This block samples the continuous-time, Real input signal u and provides it as clocked output signal y. The clock of the output signal is inferred (that is, it needs to be defined somewhere else in the clocked partition). If this is not desired, use block SampleClocked instead, to explicitly assign a clock to the output signal.
To be more precise: The input signal u(t) must be a
continuous-time signal. The output signal y(ti) is associated to a
clock (defined somewhere else). At a clock tick, the left limit of
u is assigned to y: y(ti) = u(ti-eps) (= the value of
u just before the clock became active). Since the operator returns
the left limit of u, it introduces an infinitesimal small delay
between the continuous-time and the clocked partition. This
corresponds to the reality, where a sampled data system cannot act
infinitely fast and even for a very idealized simulation, an
infinitesimal small delay is present. As a result, algebraic loops
between clocked and continuous-time partitions cannot occur.
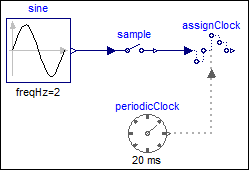
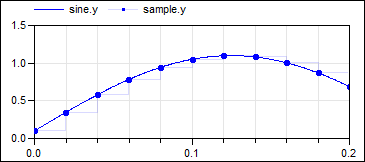
The following
example samples a sine signal with a periodic clock of 20 ms
period:
 |
 |
|
| model | simulation result |
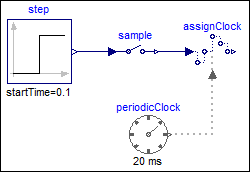
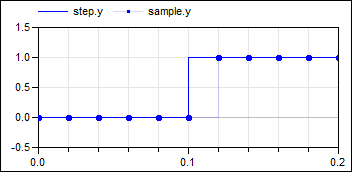
In the following
example the continuous-time input signal contains a
discontinuous value change at the 0.1 s clock tick. It can be seen
that the Sample block samples the left limit of the step
signal:
 |
 |
|
| model | simulation result |
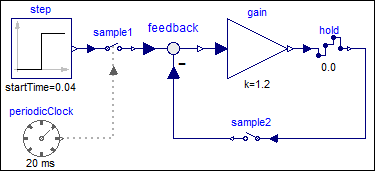
In the following
example a direct feedthrough in the continuous-time and in the
clocked partition is present. Without a time-delay, this would
result in an algebraic loop. However, since block Sample samples
the left limit of a continuous-time signal, sampling introduces a
delay of one sample period that breaks the algebraic
loop:
 |
|
| model |
|
 |
|
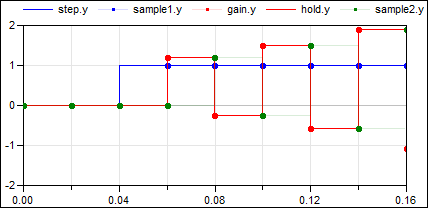
| simulation result |
Note, the reason for the delay is that sample2.y (= the green, clocked signal) is the left limit of hold.y (= the red, continuous-time signal).