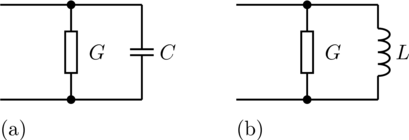
The admittance model represents a parallel
connection of a resistor and either a capacitor or inductor in each
phase.

The linear admittance connects the complex voltage
v with the complex current
i by v*Y = i
in each phase, using m
variable single-phase admittances. The admittances Y_ref
= G_ref + j*B_ref are given as complex input signals,
representing the resistive and reactive components of the input
admittances. The resistive components are modeled temperature
dependent, so the real part G_actual = real(Y)
are determined from the actual operating temperatures and the
reference input conductances real(Y_ref).
Conditional heat ports are considered. The reactive components
B_actual = imag(Y) are equal to
imag(Y_ref) if frequencyDependent =
false. Frequency dependency is considered by
frequencyDependent = true, distinguishing two
cases:
imag(Y_ref) > 0: capacitive caseB_actual are proportional
to f/f_refimag(Y_ref) < 0: inductive caseB_actual are proportional
to f_ref/fZero crossings of the real or imaginary parts of the admittance
signals Y_ref could cause singularities due to the
actual structure of the connected network.
VariableResistor, Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable conductor, Variable capacitor, Variable inductor Variable impedance,