.Modelica.Electrical.QuasiStatic.UsersGuide.Overview.Power

Information

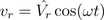
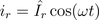
For periodic waveforms, the average value of the instantaneous power is real power P. Reactive power Q is a term associated with inductors and capacitors. For pure inductors and capacitors, real power is equal to zero. Yet, there is instantaneous power exchanged with connecting network.

Power of a resistor

The instantaneous voltage and current are in phase:

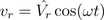
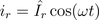
Therefore, the instantaneous power is

A graphical representation of these equations is depicted in Fig. 1

Fig. 1: Instantaneous voltage, current of power of a resistor

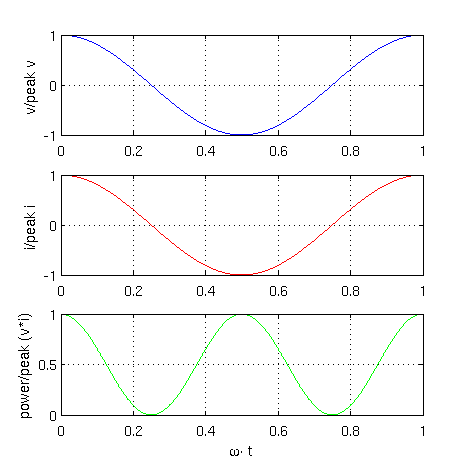Real power of the resistor is the average of instantaneous power:

Power of an inductor

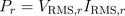
The instantaneous voltage leads the current by a quarter of the period:

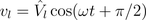
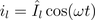
Therefore, the instantaneous power is

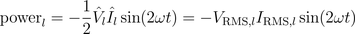
A graphical representation of these equations is depicted in Fig. 2

Fig. 2: Instantaneous voltage, current of power of an inductor

Reactive power of the inductor is:

Power of a capacitor

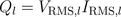
The instantaneous voltage lags the current by a quarter of the period:

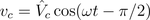
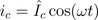
Therefore, the instantaneous power is

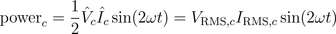
A graphical representation of these equations is depicted in Fig. 3

Fig. 3: Instantaneous voltage, current of power of a capacitor

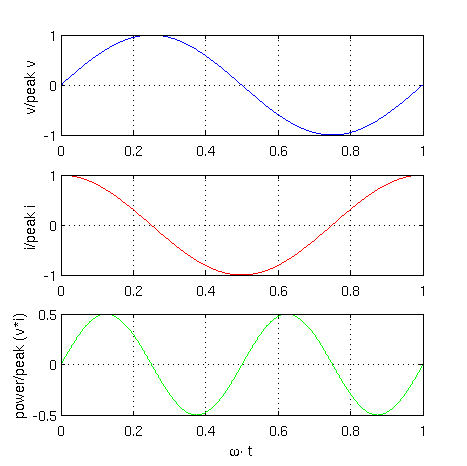Reactive power of the capacitor is:

Complex apparent power

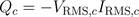
For an arbitrary component with two pins, real and reactive power can be determined by the complex phasors:

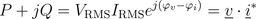
In this equation ^* represents the conjugate complex operator

See also