Calculation of the mean convective heat transfer coefficient kc for a laminar fluid flow over an even surface.
There are basically three differences:
The mean convective heat transfer coefficient kc for flat plate is calculated through the corresponding Nusselt number Nu_lam according to [VDI 2002, p. Gd 1, eq. 1] :
Nu_lam = 0.664 * Re^(0.5) * (Pr)^(1/3)
and the corresponding mean convective heat transfer coefficient kc:
kc = Nu_lam * lambda / L
with
| cp | as specific heat capacity at constant pressure [J/(kg.K)], |
| eta | as dynamic viscosity of fluid [Pa.s], |
| kc | as mean convective heat transfer coefficient [W/(m2.K)], |
| lambda | as heat conductivity of fluid [W/(m.K)], |
| L | as length of plate [m], |
| Nu_lam | as mean Nusselt number for laminar regime [-], |
| Pr = eta*cp/lambda | as Prandtl number [-], |
| rho | as fluid density [kg/m3], |
| Re = rho*v*L/eta | as Reynolds number [-]. |
The mean Nusselt number Nu in the laminar regime representing the mean convective heat transfer coefficient kc for Prandtl numbers of different fluids is shown in the figure below.
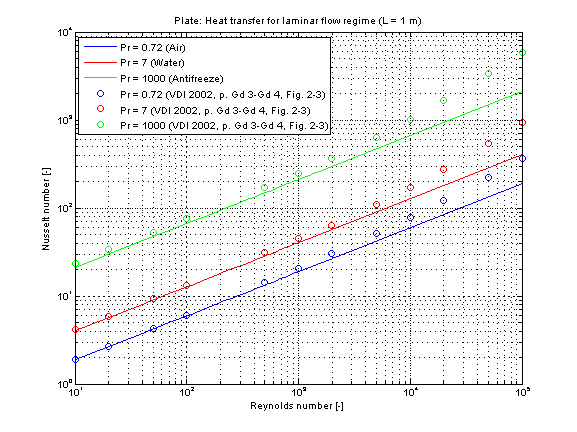
Note that this function is best used in the laminar regime up to a Reynolds number Re smaller than 2300. There is a deviation w.r.t. literature due to the neglect of the turbulence influence in the transition regime even though this function is used inside its cited restrictions for a higher Reynolds number. The function kc_overall is recommended for the simulation of a Reynolds number higher than 2300.