.Symmetrical three-phases systems of currents (or voltages)
consists of three sinusoidal sine waves with an angular
displacement of
.
,
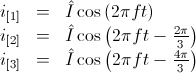Electrical three-phase machines have (usually) symmetrical
three-phase windings which excite spatial magnetic potential with a
spacial displacement of
- with respect to the fundamental wave, see [Laughton02].
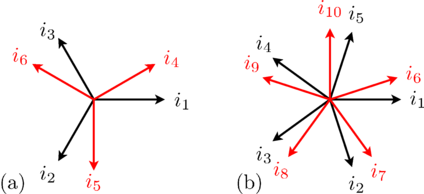
Such a symmetrical three-phase system of currents (or voltages) can
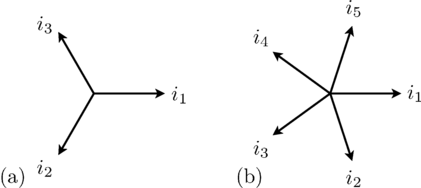
be represented by phasors, as depicted in
Fig. 1(a). The associated three-phase winding is depicted in Fig.
2(a). The winding axis are displaced by
:
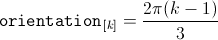
So there is a strong coherence between angular displacement in the time and spatial domain which also applies to polyphase systems.
 |
 |
In symmetrical polyphase systems odd and even phase numbers have to be distinguished.
For a symmetrical polyphase system with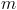 
phases the displacement in the time and spatial domain is
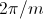, as depicted in Fig. 1 and 2.
Mathematically, this symmetry is expressed in terms of phase currents by:
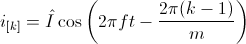
The orientation of the winding axis of such winding is given by:
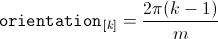
In the current implementation of the FundamentalWave library,
phase numbers equal to the power of two are not supported. However,
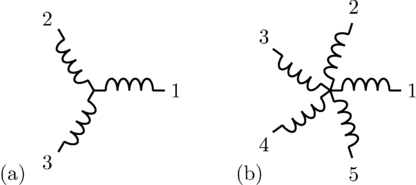
any other polyphase system with even an phase number,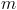
, can be recursively split into various symmetrical systems with
odd phase numbers, as depicted in Fig. 3 and 4. The displacement
between the two symmetrical systems is 
. A function for calculating the
symmetricOrientation is available.
 |
 |
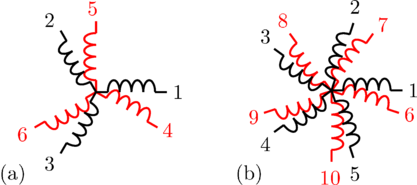In a fully symmetrical machine, the orientation of the winding axes and the symmetrical currents (or voltages) phasors have different signs; see Fig. 1 and 2 for odd phase numbers and Fig. 3 and 4 for even phase numbers.