Modelica.Magnetic.QuasiStatic.FluxTubes.UsersGuide

The quasi static flux tubes library is based on the transient library Magnetic.FluxTubes. The main principles of confined flux and flux tubes apply, too. The quasi static flux tubes library contains components for modelling of electromagnetic devices with lumped magnetic networks based on quasi static theory. Models based on this library are suited for quasi static simulation of transformers at component and system level.

The quasi static components of this library do not consider saturation since linearity is strictly assumed. In case that the permeability of a saturated circuit needs to be considered, a transient permeability estimation sensor is provided do determine the effective permeability from a transient simulation.

A general introduction into quasi static (quasi stationary) phasor can be found in Modelica.Electrical.QuasiStationary.

This user's guide gives a short introduction to the underlying concept of quasi static magnetic flux tubes, summarizes basic relationships and equations.

Extends from Modelica.Icons.Information (Icon for general information packages).

Package Content

Name	Description
FluxTubeConcept	Flux tube concept
Literature	Literature
ReleaseNotes	Release Notes
Contact	Contact

Modelica.Magnetic.QuasiStatic.FluxTubes.UsersGuide.FluxTubeConcept

Overview of the concept of quasi static magnetic flux tubes

Following below, the concept of magnetic flux tubes is outlined in short. For a detailed description of flux tube elements, please have a look at the listed literature. Magnetic flux tubes enable the modeling of magnetic fields with lumped equivalent circuit networks.

Since quasi static conditions are assumed, each field quantity can be represented by a complex phasor -- which is indicated by underlining the respective variable:

• Normal component of magnetic flux density,
• Normal component of magnetic field strength,
• Magnetic flux,
• Magnetic potential difference,

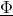
The figure below and the following equations illustrate the relationships between

• the normal component of flux density and magnetic flux, and
• the normal component of field strength and magnetic potential difference.

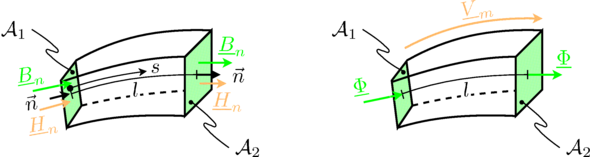
A flux tube confines the magnetic flux. Flied lines, and flux tubes, respectively are always closed. So there is no flux entering or leaving a flux tube. The total flux of a configuration can be represented by parallel flux tubes, representing different flux paths. This is considered by connecting the elements of a lumped circuit model, such that the sum of all fluxes of a connection is equivalent to zero.

For a section of a flux tube with length the magnetic potential difference is determined by the length integral over the magnetic field strength:

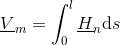
The magnetic flux entering, and leaving a flux tube, respectively, is determined by the surface integral of the normal component of the magnetic field strength:

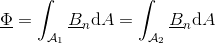
The magnetic potential difference and the magnetic flux have the same angle, so the reluctance a real (non complex) quantity:

For a generic flux tube reluctance with constant area of cross section, 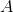, and length, 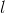, the magnetic reluctance is:

Assumptions

• Force interaction is not considered
• Reluctance models are linear; so non-linearities can only be taken into account by adapting the constant relative permeability; see example NonLinearInductor

Notes

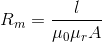
The parameter and variable names are chosen as close as possible to the transient FluxTubes library, to avoid additional effort when converting transient into quasi static flux tubes models.

Reference Note

A similar approach on quasi static flux tube models is published in [Raabe2012].

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Magnetic.QuasiStatic.FluxTubes.UsersGuide.Literature

References

Additional References

Additional reference on magnetic flux tubes are listed in Modelica.Magnetic.FluxTubes.

Extends from Modelica.Icons.References (Icon for external references).

Modelica.Magnetic.QuasiStatic.FluxTubes.UsersGuide.ReleaseNotes

Version 3.2.3, 2019-01-23

• Included in the MSL 3.2.3
• Added some more examples according to #1515
• Added magnitudes and angles of complex quantities for better result interpretation

Version 1.0.0, 2013-12-18

• Initial version before inclusion in MSL

Extends from Modelica.Icons.ReleaseNotes (Icon for release notes in documentation).

Modelica.Magnetic.QuasiStatic.FluxTubes.UsersGuide.Contact

Contact

Dr. Christian Kral
Electric Machines, Drives and Systems
A-1060 Vienna, Austria
email: dr.christian.kral@gmail.com

Anton Haumer
Technical Consulting & Electrical Engineering
D-93049 Regensburg, Germany
email: a.haumer@haumer.at

Extends from Modelica.Icons.Contact (Icon for contact information).