Package Modelica.​Mechanics.​MultiBody
Library to model 3-dimensional mechanical systems

Information

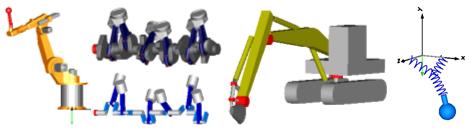
Library MultiBody is a free Modelica package providing 3-dimensional mechanical components to model in a convenient way mechanical systems, such as robots, mechanisms, vehicles. Typical animations generated with this library are shown in the next figure:

For an introduction, have especially a look at:

• MultiBody.UsersGuide discusses the most important aspects how to use this library.
• MultiBody.Examples contains examples that demonstrate the usage of this library.

Copyright © 1998-2018, Modelica Association and contributors

Extends from Modelica.​Icons.​Package (Icon for standard packages).

Package Contents

Model Modelica.​Mechanics.​MultiBody.​World
World coordinate system + gravity field + default animation definition

Information

Model World represents a global coordinate system fixed in ground. This model serves several purposes:

• It is used as inertial system in which the equations of all elements of the MultiBody library are defined.
• It is the world frame of an animation window in which all elements of the MultiBody library are visualized.
• It is used to define the gravity field in which a multi-body model is present. Default is a uniform gravity field where the gravity acceleration vector g is the same at every position. Additionally, a point gravity field or no gravity can be selected. Also, function gravityAcceleration can be redeclared to a user-defined function that computes the gravity acceleration, see example Examples.Elementary.UserDefinedGravityField.
• It is used to define default settings of animation properties (e.g., the diameter of a sphere representing by default the center of mass of a body, or the diameters of the cylinders representing a revolute joint).
• It is used to define a visual representation of the world model (= 3 coordinate axes with labels), of the defined gravity field and of a ground plane perpendicular to the gravity direction.
  

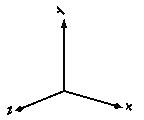
Since the gravity field function is required from all bodies with mass and the default settings of animation properties are required from nearly every component, exactly one instance of model World needs to be present in every model on the top level. The basic declaration needs to be:

inner Modelica.Mechanics.MultiBody.World world

Note, it must be an inner declaration with instance name world in order that this world object can be accessed from all objects in the model. When dragging the "World" object from the package browser into the diagram layer, this declaration is automatically generated (this is defined via annotations in model World).

All vectors and tensors of a mechanical system are resolved in a frame that is local to the corresponding component. Usually, if all relative joint coordinates vanish, the local frames of all components are parallel to each other, as well as to the world frame (this holds as long as a Parts.FixedRotation, component is not used). In this "reference configuration" it is therefore alternatively possible to resolve all vectors in the world frame, since all frames are parallel to each other. This is often very convenient. In order to give some visual support in such a situation, in the icon of a World instance two axes of the world frame are shown and the labels of these axes can be set via parameters.

Parameters

Connectors

Generated 2018-12-12 12:12:55 EST by MapleSim.