This information is part of the Modelica Standard Library maintained by the Modelica Association.

Calculation of pressure loss in a straight pipe for laminar flow regime of single-phase fluid flow only.

Restriction

This function shall be used inside of the restricted limits according to the referenced literature.

• circular cross sectional area
• laminar flow regime (Reynolds number Re ≤ 2000) [VDI-Wärmeatlas 2002, p. Lab, eq. 3]

Geometry

Calculation

The pressure loss dp for straight pipes is determined by:

    dp = lambda_FRI * (L/d_hyd) * (rho/2) * velocity^2

with

lambda_FRI	as Darcy friction factor [-].
L	as length of straight pipe [m],
d_hyd	as hydraulic diameter of straight pipe [m],
rho	as density of fluid [kg/m3],
velocity	as mean velocity [m/s].

The Darcy friction factor lambda_FRI of straight pipes for the laminar flow regime is calculated by Hagen-Poiseuilles law according to [Idelchik 2006, p. 77, eq. 2-3] as follows:

• Laminar flow regime is restricted to a Reynolds number Re ≤ 2000
• and calculated through:

       lambda_FRI = 64/Re
       

  with

  lambda_FRI	as Darcy friction factor [-],
  Re	as Reynolds number [-].

The Darcy friction factor lambda_FRI in the laminar regime is independent of the surface roughness K as long as the relative roughness k = surface roughness/hydraulic diameter is smaller than 0.007. A higher relative roughness k than 0.007 leads to an earlier leaving of the laminar regime to the transition regime at some value of Reynolds number Re_lam_leave . This earlier leaving is not modelled here because only laminar fluid flow is considered.

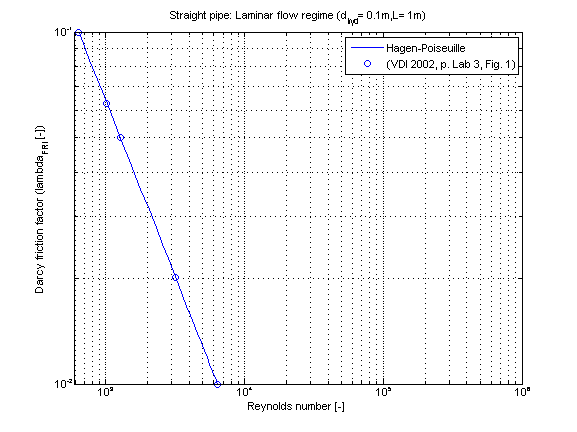
Verification

The Darcy friction factor lambda_FRI in dependence of Reynolds number is shown in the figure below.

The pressure loss dp for the laminar regime in dependence of the mass flow rate of water is shown in the figure below.

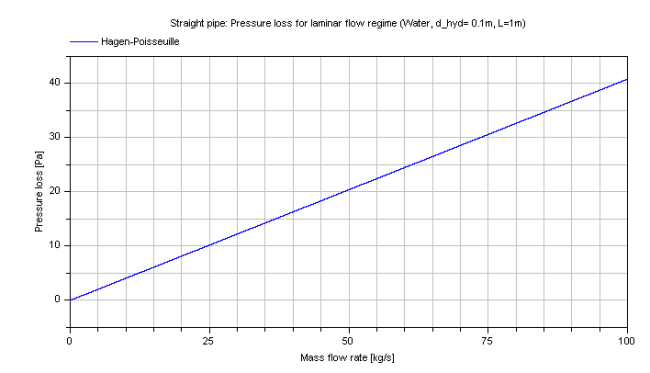
Note that this pressure loss function shall not be used for the modelling outside of the laminar flow regime at Re > 2000 even though it could be used for that.

If the whole flow regime shall be modelled, the pressure loss function dp_overall can be used.

References

Elmqvist,H., M.Otter and S.E. Cellier:

Inline integration: A new mixed symbolic / numeric approach for solving differential-algebraic equation systems.. In Proceedings of European Simulation MultiConference, Praque, 1995.

Idelchik,I.E.:

Handbook of hydraulic resistance. Jaico Publishing House, Mumbai, 3rd edition, 2006.

VDI:

VDI - Wärmeatlas: Berechnungsblätter für den Wärmeübergang. Springer Verlag, 9th edition, 2002.