This information is part of the Modelica Standard Library maintained by the Modelica Association.

Approximates the function

   y = if x ≥ 0 then sqrt(k1*x) else -sqrt(k2*abs(x)), with k1, k2 ≥ 0

in such a way that within the region -x_small ≤ x ≤ x_small, the function is described by two polynomials of third order (one in the region -x_small .. 0 and one within the region 0 .. x_small) such that

• The derivative at x=0 is finite.
• The overall function is continuous with a continuous first derivative everywhere.
• If parameter use_yd0 = false, the two polynomials are constructed such that the second derivatives at x=0 are identical. If use_yd0 = true, the derivative at x=0 is explicitly provided via the additional argument yd0. If necessary, the derivative yd0 is automatically reduced in order that the polynomials are strict monotonically increasing [Fritsch and Carlson, 1980].

Typical screenshots for two different configurations are shown below. The first one with k1=k2=1:

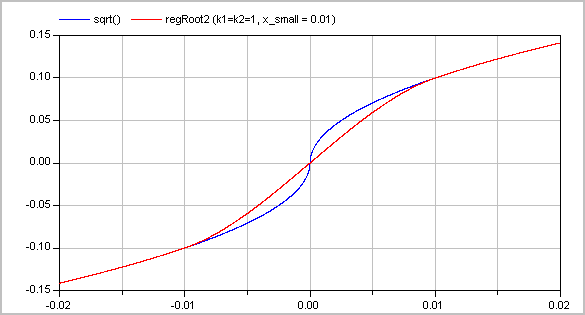
and the second one with k1=1 and k2=3:

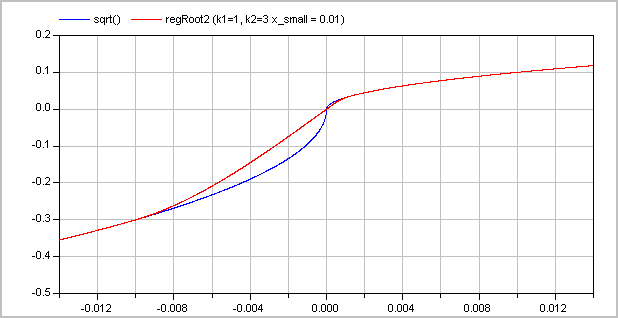
The (smooth) derivative of the function with k1=1, k2=3 is shown in the next figure:

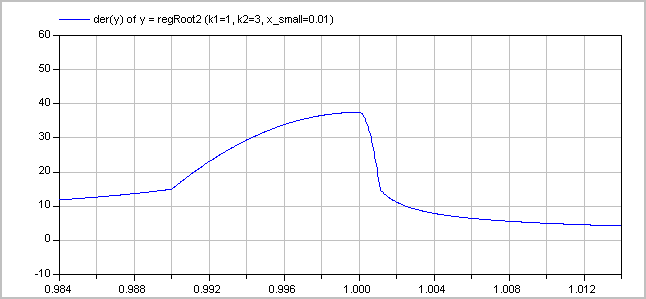
Literature

Fritsch F.N. and Carlson R.E. (1980):

Monotone piecewise cubic interpolation. SIAM J. Numerc. Anal., Vol. 17, No. 2, April 1980, pp. 238-246

y = regRoot2(x, x_small, k1, k2, use_yd0, yd0)

x	Type: Real Description: abscissa value
x_small	Default Value: 0.01 Type: Real Description: approximation of function for |x| <= x_small
k1	Default Value: 1 Type: Real Description: y = if x>=0 then sqrt(k1*x) else -sqrt(k2*|x|)
k2	Default Value: 1 Type: Real Description: y = if x>=0 then sqrt(k1*x) else -sqrt(k2*|x|)
use_yd0	Default Value: false Type: Boolean Description: = true, if yd0 shall be used
yd0	Default Value: 1 Type: Real Description: Desired derivative at x=0: dy/dx = yd0

y	Type: Real Description: ordinate value