Modelica.Blocks.Continuous

Library of continuous control blocks with internal states

Information

This package contains basic continuous input/output blocks described by differential equations.

All blocks of this package can be initialized in different ways controlled by parameter initType. The possible values of initType are defined in Modelica.Blocks.Types.Init:

For backward compatibility reasons the default of all blocks is Init.NoInit, with the exception of Integrator and LimIntegrator where the default is Init.InitialState (this was the initialization defined in version 2.2 of the Modelica standard library).

In many cases, the most useful initial condition is Init.SteadyState because initial transients are then no longer present. The drawback is that in combination with a non-linear plant, non-linear algebraic equations occur that might be difficult to solve if appropriate guess values for the iteration variables are not provided (i.e., start values with fixed=false). However, it is often already useful to just initialize the linear blocks from the Continuous blocks library in SteadyState. This is uncritical, because only linear algebraic equations occur. If Init.NoInit is set, then the start values for the states are interpreted as guess values and are propagated to the states with fixed=false.

Note, initialization with Init.SteadyState is usually difficult for a block that contains an integrator (Integrator, LimIntegrator, PI, PID, LimPID). This is due to the basic equation of an integrator:

initial equation
   der(y) = 0;   // Init.SteadyState
equation
   der(y) = k*u;

The steady state equation leads to the condition that the input to the integrator is zero. If the input u is already (directly or indirectly) defined by another initial condition, then the initialization problem is singular (has none or infinitely many solutions). This situation occurs often for mechanical systems, where, e.g., u = desiredSpeed - measuredSpeed and since speed is both a state and a derivative, it is always defined by Init.InitialState or Init.SteadyState initialization.

In such a case, Init.NoInit has to be selected for the integrator and an additional initial equation has to be added to the system to which the integrator is connected. E.g., useful initial conditions for a 1-dim. rotational inertia controlled by a PI controller are that angle, speed, and acceleration of the inertia are zero.

Extends from Modelica.Icons.Package (Icon for standard packages).

Package Content

Name	Description
Integrator	Output the integral of the input signal with optional reset
LimIntegrator	Integrator with limited value of the output and optional reset
Derivative	Approximated derivative block
FirstOrder	First order transfer function block (= 1 pole)
SecondOrder	Second order transfer function block (= 2 poles)
PI	Proportional-Integral controller
PID	PID-controller in additive description form
LimPID	P, PI, PD, and PID controller with limited output, anti-windup compensation, setpoint weighting and optional feed-forward
TransferFunction	Linear transfer function
StateSpace	Linear state space system
Der	Derivative of input (= analytic differentiations)
LowpassButterworth	Output the input signal filtered with a low pass Butterworth filter of any order
CriticalDamping	Output the input signal filtered with an n-th order filter with critical damping
Filter	Continuous low pass, high pass, band pass or band stop IIR-filter of type CriticalDamping, Bessel, Butterworth or ChebyshevI
Internal	Internal utility functions and blocks that should not be directly utilized by the user

Modelica.Blocks.Continuous.Integrator

Output the integral of the input signal with optional reset

Information

This blocks computes output y as integral of the input u multiplied with the gain k:

    k
y = - u
    s

It might be difficult to initialize the integrator in steady state. This is discussed in the description of package Continuous.

If the reset port is enabled, then the output y is reset to set or to y_start (if the set port is not enabled), whenever the reset port has a rising edge.

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica.Blocks.Continuous.LimIntegrator

Integrator with limited value of the output and optional reset

Information

This blocks computes y as integral of the input u multiplied with the gain k. If the integral reaches a given upper or lower limit and the input will drive the integral outside of this bound, the integration is halted and only restarted if the input drives the integral away from the bounds.

It might be difficult to initialize the integrator in steady state. This is discussed in the description of package Continuous.

If parameter limitsAtInit = false, the limits of the integrator are removed from the initialization problem which leads to a much simpler equation system. After initialization has been performed, it is checked via an assert whether the output is in the defined limits. For backward compatibility reasons limitsAtInit = true. In most cases it is best to use limitsAtInit = false.

If the reset port is enabled, then the output y is reset to set or to y_start (if the set port is not enabled), whenever the reset port has a rising edge.

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica.Blocks.Continuous.Derivative

Approximated derivative block

Information

This blocks defines the transfer function between the input u and the output y as approximated derivative:

        k * s
y = ------------ * u
       T * s + 1

If you would like to be able to change easily between different transfer functions (FirstOrder, SecondOrder, ... ) by changing parameters, use the general block TransferFunction instead and model a derivative block with parameters
b = {k,0}, a = {T, 1}.

If k=0, the block reduces to y=0.

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica.Blocks.Continuous.FirstOrder

First order transfer function block (= 1 pole)

Information

This blocks defines the transfer function between the input u and the output y as first order system:

          k
y = ------------ * u
       T * s + 1

If you would like to be able to change easily between different transfer functions (FirstOrder, SecondOrder, ... ) by changing parameters, use the general block TransferFunction instead and model a first order SISO system with parameters
b = {k}, a = {T, 1}.

Example:
   parameter: k = 0.3, T = 0.4
   results in:
             0.3
      y = ----------- * u
          0.4 s + 1.0

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica.Blocks.Continuous.SecondOrder

Second order transfer function block (= 2 poles)

Information

This blocks defines the transfer function between the input u and the output y as second order system:

                    k
y = --------------------------------- * u
     ( s / w )^2 + 2*D*( s / w ) + 1

If you would like to be able to change easily between different transfer functions (FirstOrder, SecondOrder, ... ) by changing parameters, use the general model class TransferFunction instead and model a second order SISO system with parameters
b = {k}, a = {1/w^2, 2*D/w, 1}.

Example:

   parameter: k =  0.3,  w = 0.5,  D = 0.4
   results in:
                  0.3
      y = ------------------- * u
          4.0 s^2 + 1.6 s + 1

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica.Blocks.Continuous.PI

Proportional-Integral controller

Information

This blocks defines the transfer function between the input u and the output y as PI system:

              1
y = k * (1 + ---) * u
             T*s
        T*s + 1
  = k * ------- * u
          T*s

If you would like to be able to change easily between different transfer functions (FirstOrder, SecondOrder, ... ) by changing parameters, use the general model class TransferFunction instead and model a PI SISO system with parameters
b = {k*T, k}, a = {T, 0}.

Example:

   parameter: k = 0.3,  T = 0.4

   results in:
               0.4 s + 1
      y = 0.3 ----------- * u
                 0.4 s

It might be difficult to initialize the PI component in steady state due to the integrator part. This is discussed in the description of package Continuous.

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica.Blocks.Continuous.PID

PID-controller in additive description form

Information

This is the text-book version of a PID-controller. For a more practically useful PID-controller, use block LimPID.

The PID block can be initialized in different ways controlled by parameter initType. The possible values of initType are defined in Modelica.Blocks.Types.Init.

Based on the setting of initType, the integrator (I) and derivative (D) blocks inside the PID controller are initialized according to the following table:

In many cases, the most useful initial condition is SteadyState because initial transients are then no longer present. If initType = Init.SteadyState, then in some cases difficulties might occur. The reason is the equation of the integrator:

der(y) = k*u;

The steady state equation "der(x)=0" leads to the condition that the input u to the integrator is zero. If the input u is already (directly or indirectly) defined by another initial condition, then the initialization problem is singular (has none or infinitely many solutions). This situation occurs often for mechanical systems, where, e.g., u = desiredSpeed - measuredSpeed and since speed is both a state and a derivative, it is natural to initialize it with zero. As sketched this is, however, not possible. The solution is to not initialize u or the variable that is used to compute u by an algebraic equation.

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica.Blocks.Continuous.LimPID

P, PI, PD, and PID controller with limited output, anti-windup compensation, setpoint weighting and optional feed-forward

Information

Via parameter controllerType either P, PI, PD, or PID can be selected. If, e.g., PI is selected, all components belonging to the D-part are removed from the block (via conditional declarations). The example model Modelica.Blocks.Examples.PID_Controller demonstrates the usage of this controller. Several practical aspects of PID controller design are incorporated according to chapter 3 of the book:

Åström K.J., and Hägglund T.:

PID Controllers: Theory, Design, and Tuning. Instrument Society of America, 2nd edition, 1995.

Besides the additive proportional, integral and derivative part of this controller, the following features are present:

• The output of this controller is limited. If the controller is in its limits, anti-windup compensation is activated to drive the integrator state to zero.
• The high-frequency gain of the derivative part is limited to avoid excessive amplification of measurement noise.
• Setpoint weighting is present, which allows to weight the setpoint in the proportional and the derivative part independently from the measurement. The controller will respond to load disturbances and measurement noise independently of this setting (parameters wp, wd). However, setpoint changes will depend on this setting. For example, it is useful to set the setpoint weight wd for the derivative part to zero, if steps may occur in the setpoint signal.
• Optional feed-forward. It is possible to add a feed-forward signal. The feed-forward signal is added before limitation.

The parameters of the controller can be manually adjusted by performing simulations of the closed loop system (= controller + plant connected together) and using the following strategy:

1. Set very large limits, e.g., yMax = Modelica.Constants.inf
2. Select a P-controller and manually enlarge parameter k (the total gain of the controller) until the closed-loop response cannot be improved any more.
3. Select a PI-controller and manually adjust parameters k and Ti (the time constant of the integrator). The first value of Ti can be selected, such that it is in the order of the time constant of the oscillations occurring with the P-controller. If, e.g., vibrations in the order of T=10 ms occur in the previous step, start with Ti=0.01 s.
4. If you want to make the reaction of the control loop faster (but probably less robust against disturbances and measurement noise) select a PID-Controller and manually adjust parameters k, Ti, Td (time constant of derivative block).
5. Set the limits yMax and yMin according to your specification.
6. Perform simulations such that the output of the PID controller goes in its limits. Tune Ni (Ni*Ti is the time constant of the anti-windup compensation) such that the input to the limiter block (= limiter.u) goes quickly enough back to its limits. If Ni is decreased, this happens faster. If Ni=infinity, the anti-windup compensation is switched off and the controller works bad.

Initialization

This block can be initialized in different ways controlled by parameter initType. The possible values of initType are defined in Modelica.Blocks.Types.Init.

Based on the setting of initType, the integrator (I) and derivative (D) blocks inside the PID controller are initialized according to the following table:

In many cases, the most useful initial condition is SteadyState because initial transients are then no longer present. If initType = Init.SteadyState, then in some cases difficulties might occur. The reason is the equation of the integrator:

der(y) = k*u;

The steady state equation "der(x)=0" leads to the condition that the input u to the integrator is zero. If the input u is already (directly or indirectly) defined by another initial condition, then the initialization problem is singular (has none or infinitely many solutions). This situation occurs often for mechanical systems, where, e.g., u = desiredSpeed - measuredSpeed and since speed is both a state and a derivative, it is natural to initialize it with zero. As sketched this is, however, not possible. The solution is to not initialize u_m or the variable that is used to compute u_m by an algebraic equation.

When initializing in steady-state, homotopy-based initialization can help the convergence of the solver, by using a simplified model a the beginning of the solution process. Different options are available.

• homotopyType=Linear (default): the limitations are removed from the simplified model, making it linear. Use this if you know that the controller will not be saturated at steady state.
• homotopyType=UpperLimit: if it is known a priori the controller will be stuck at the upper limit yMax, this option assumes y = yMax as a simplified model.
• homotopyType=LowerLimit: if it is known a priori the controller will be stuck at the lower limit yMin, this option assumes y = yMin as a simplified model.
• homotopyType=NoHomotopy: this option does not apply any simplification and keeps the limiter active throughout the homotopy transformation. Use this if it is unknown whether the controller is saturated or not at initialization and if the limitations on the output must be enforced throughout the entire homotopy transformation.

Extends from Modelica.Blocks.Interfaces.SVcontrol (Single-Variable continuous controller).

Parameters

Connectors

Modelica.Blocks.Continuous.TransferFunction

Linear transfer function

Information

This block defines the transfer function between the input u and the output y as (nb = dimension of b, na = dimension of a):

        b[1]*s^[nb-1] + b[2]*s^[nb-2] + ... + b[nb]
y(s) = --------------------------------------------- * u(s)
        a[1]*s^[na-1] + a[2]*s^[na-2] + ... + a[na]

State variables x are defined according to controller canonical form. Internally, vector x is scaled to improve the numerics (the states in versions before version 3.0 of the Modelica Standard Library have been not scaled). This scaling is not visible from the outside of this block because the non-scaled vector x is provided as output signal and the start value is with respect to the non-scaled vector x. Initial values of the states x can be set via parameter x_start.

Example:

TransferFunction g(b = {2,4}, a = {1,3});

results in the following transfer function:

     2*s + 4
y = --------- * u
      s + 3

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica.Blocks.Continuous.StateSpace

Linear state space system

Information

The State Space block defines the relation between the input u and the output y in state space form:

der(x) = A * x + B * u
    y  = C * x + D * u

The input is a vector of length nu, the output is a vector of length ny and nx is the number of states. Accordingly

A has the dimension: A(nx,nx),
B has the dimension: B(nx,nu),
C has the dimension: C(ny,nx),
D has the dimension: D(ny,nu)

Example:

parameter: A = [0.12, 2;3, 1.5]
parameter: B = [2, 7;3, 1]
parameter: C = [0.1, 2]
parameter: D = zeros(ny,nu)

results in the following equations:
  [der(x[1])]   [0.12  2.00] [x[1]]   [2.0  7.0] [u[1]]
  [         ] = [          ]*[    ] + [        ]*[    ]
  [der(x[2])]   [3.00  1.50] [x[2]]   [0.1  2.0] [u[2]]
                             [x[1]]            [u[1]]
       y[1]   = [0.1  2.0] * [    ] + [0  0] * [    ]
                             [x[2]]            [u[2]]

Extends from Interfaces.MIMO (Multiple Input Multiple Output continuous control block).

Parameters

Connectors

Modelica.Blocks.Continuous.Der

Derivative of input (= analytic differentiations)

Information

Defines that the output y is the derivative of the input u. Note, that Modelica.Blocks.Continuous.Derivative computes the derivative in an approximate sense, where as this block computes the derivative exactly. This requires that the input u is differentiated by the Modelica translator, if this derivative is not yet present in the model.

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Connectors

Modelica.Blocks.Continuous.LowpassButterworth

Output the input signal filtered with a low pass Butterworth filter of any order

Information

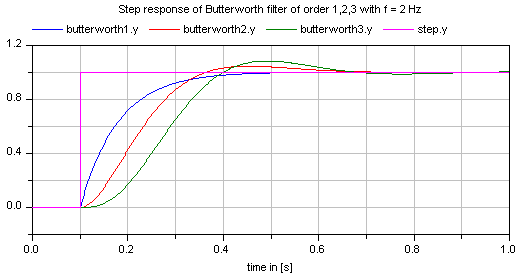
This block defines the transfer function between the input u and the output y as an n-th order low pass filter with Butterworth characteristics and cut-off frequency f. It is implemented as a series of second order filters and a first order filter. Butterworth filters have the feature that the amplitude at the cut-off frequency f is 1/sqrt(2) (= 3 dB), i.e., they are always "normalized". Step responses of the Butterworth filter of different orders are shown in the next figure:

If transients at the simulation start shall be avoided, the filter should be initialized in steady state (e.g., using option initType=Modelica.Blocks.Types.Init.SteadyState).

Extends from Modelica.Blocks.Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica.Blocks.Continuous.CriticalDamping

Output the input signal filtered with an n-th order filter with critical damping

Information

This block defines the transfer function between the input u and the output y as an n-th order filter with critical damping characteristics and cut-off frequency f. It is implemented as a series of first order filters. This filter type is especially useful to filter the input of an inverse model, since the filter does not introduce any transients.

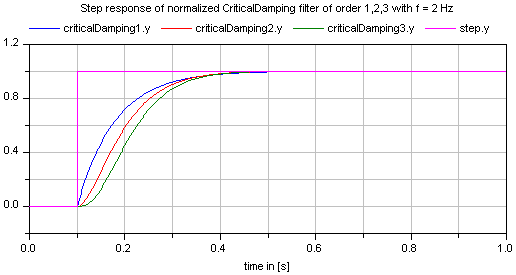
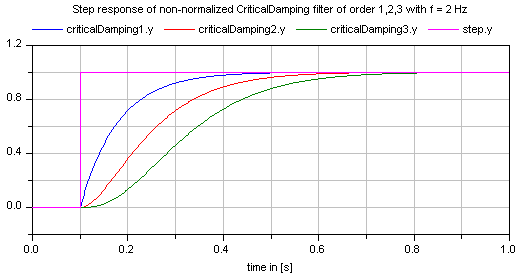
If parameter normalized = true (default), the filter is normalized such that the amplitude of the filter transfer function at the cut-off frequency f is 1/sqrt(2) (= 3 dB). Otherwise, the filter is not normalized, i.e., it is unmodified. A normalized filter is usually much better for applications, since filters of different orders are "comparable", whereas non-normalized filters usually require to adapt the cut-off frequency, when the order of the filter is changed. Figures of the filter step responses are shown below. Note, in versions before version 3.0 of the Modelica Standard library, the CriticalDamping filter was provided only in non-normalized form.

If transients at the simulation start shall be avoided, the filter should be initialized in steady state (e.g., using option initType=Modelica.Blocks.Types.Init.SteadyState).

The critical damping filter is defined as

α = if normalized then sqrt(2^(1/n) - 1) else 1 // frequency correction factor
ω = 2*π*f/α
          1
y = ------------- * u
     (s/w + 1)^n

Extends from Modelica.Blocks.Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica.Blocks.Continuous.Filter

Continuous low pass, high pass, band pass or band stop IIR-filter of type CriticalDamping, Bessel, Butterworth or ChebyshevI

Information

This blocks models various types of filters:

low pass, high pass, band pass, and band stop filters

using various filter characteristics:

CriticalDamping, Bessel, Butterworth, Chebyshev Type I filters

By default, a filter block is initialized in steady-state, in order to avoid unwanted oscillations at the beginning. In special cases, it might be useful to select one of the other initialization options under tab "Advanced".

Typical frequency responses for the 4 supported low pass filter types are shown in the next figure:

The step responses of the same low pass filters are shown in the next figure, starting from a steady state initial filter with initial input = 0.2:

Obviously, the frequency responses give a somewhat wrong impression of the filter characteristics: Although Butterworth and Chebyshev filters have a significantly steeper magnitude as the CriticalDamping and Bessel filters, the step responses of the latter ones are much better. This means for example, that a CriticalDamping or a Bessel filter should be selected, if a filter is mainly used to make a non-linear inverse model realizable.

Typical frequency responses for the 4 supported high pass filter types are shown in the next figure:

The corresponding step responses of these high pass filters are shown in the next figure:

All filters are available in normalized (default) and non-normalized form. In the normalized form, the amplitude of the filter transfer function at the cut-off frequency f_cut is -3 dB (= 10^(-3/20) = 0.70794..). Note, when comparing the filters of this function with other software systems, the setting of "normalized" has to be selected appropriately. For example, the signal processing toolbox of MATLAB provides the filters in non-normalized form and therefore a comparison makes only sense, if normalized = false is set. A normalized filter is usually better suited for applications, since filters of different orders are "comparable", whereas non-normalized filters usually require to adapt the cut-off frequency, when the order of the filter is changed. See a comparison of "normalized" and "non-normalized" filters at hand of CriticalDamping filters of order 1,2,3:

Implementation

The filters are implemented in the following, reliable way:

1. A prototype low pass filter with a cut-off angular frequency of 1 rad/s is constructed from the desired analogFilter and the desired normalization.
2. This prototype low pass filter is transformed to the desired filterType and the desired cut-off frequency f_cut using a transformation on the Laplace variable "s".
3. The resulting first and second order transfer functions are implemented in state space form, using the "eigen value" representation of a transfer function:

   // second order block with eigen values: a +/- jb
   der(x1) = a*x1 - b*x2 + (a^2 + b^2)/b*u;
   der(x2) = b*x1 + a*x2;
        y  = x2;
        

   The dc-gain from the input to the output of this block is one and the selected states are in the order of the input (if "u" is in the order of "one", then the states are also in the order of "one"). In the "Advanced" tab, a "nominal" value for the input "u" can be given. If appropriately selected, the states are in the order of "one" and then step-size control is always appropriate.

References

Tietze U., and Schenk C. (2002):

Halbleiter-Schaltungstechnik. Springer Verlag, 12. Auflage, pp. 815-852.

Extends from Modelica.Blocks.Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors