Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.HeatTransfer.HeatExchanger

Extends from Modelica.Icons.Information (Icon for general information packages).

Package Content

Name	Description
kc_flatTube
kc_roundTube

Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.HeatTransfer.HeatExchanger.kc_flatTube

Calculation of the mean convective heat transfer coefficient kc for the air-side heat transfer of heat exchangers with flat tubes and several fin geometries.

Functions kc_flatTube and kc_flatTube_KC

There are basically three differences:

• The function kc_flatTube is using kc_flatTube_KC but offers additional output variables like e.g. Reynolds number or Nusselt number and failure status (an output of 1 means that the function is not valid for the inputs).
• Generally the function kc_flatTube_KC is numerically best used for the calculation of the mean convective heat transfer coefficient kc at known mass flow rate.
• You can perform an inverse calculation from kc_flatTube_KC, where an unknown mass flow rate is calculated out of a given mean convective heat transfer coefficient kc

Restriction

• According to the kind of fin geometry the calculation is valid in a range of Re from 100 to 5000.
• medium = air

Geometry

Calculation

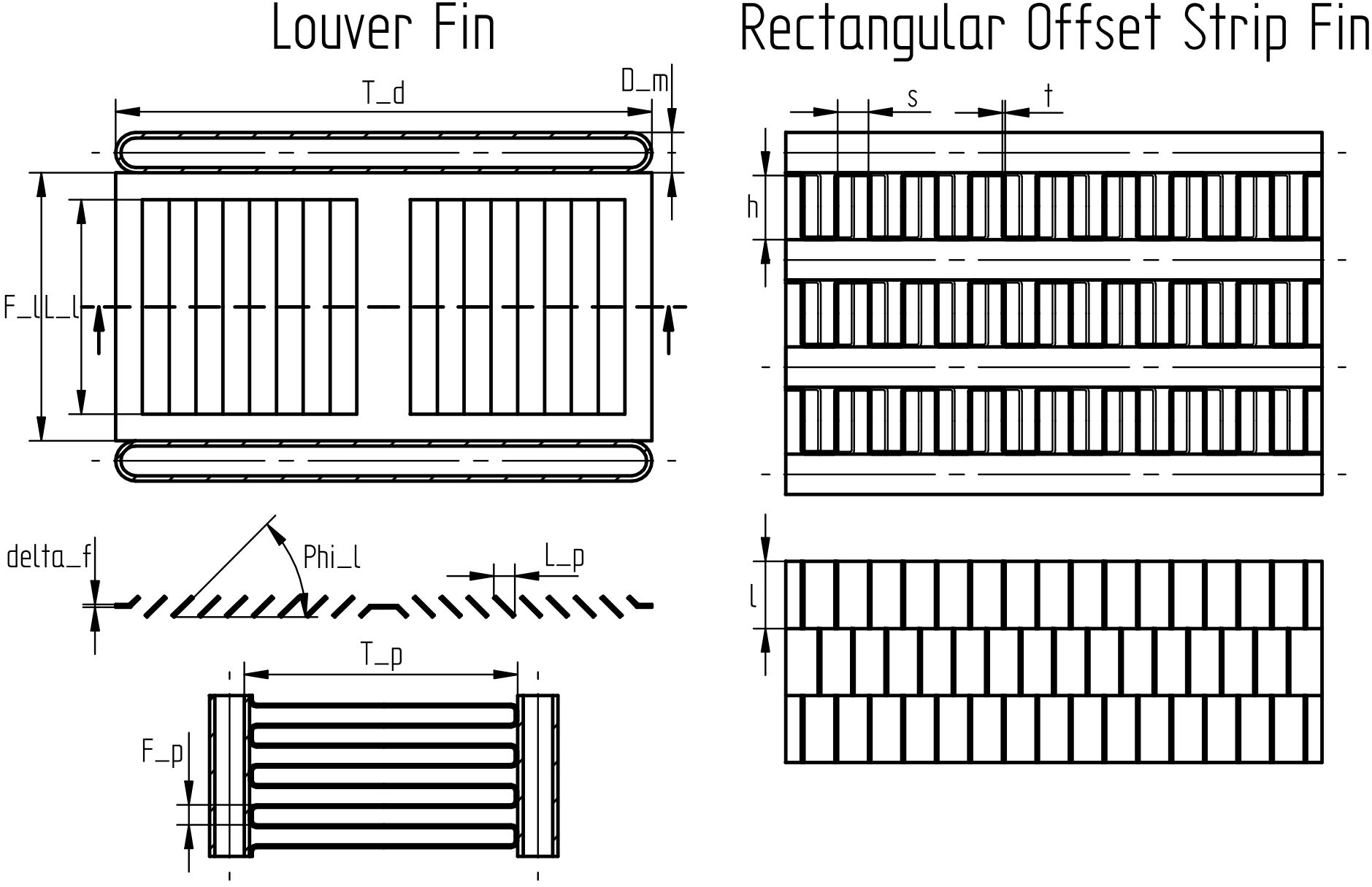
The mean convective heat transfer coefficient kc for heat exchanger is calculated through the corresponding Coulburn factor j:

j = f(geometry, Re)

with the resulting mean convective heat transfer coefficient kc

kc =  j * Re_L_p * Pr^(1/3) * lambda / L_p (Louver fin)

or

kc =  j * Re_D_h * Pr^(1/3) * lambda / D_h (Rectangular offset strip fin)

with

Verification

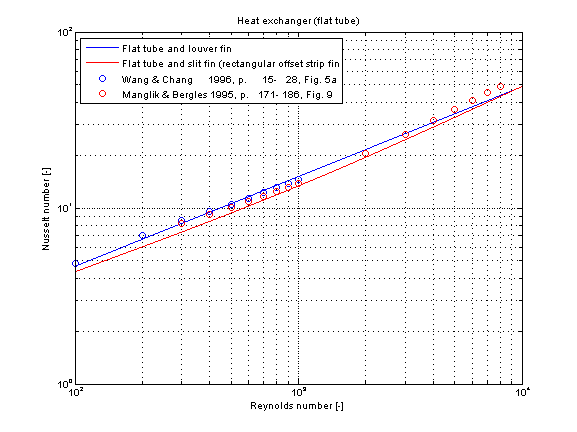
The mean Nusselt number Nu representing the mean convective heat transfer coefficient kc is shown below for different fin geometries at similar dimensions.

References

Y.-J. CHANG and C.-C. WANG:

A generalized heat transfer correlation for louver fin geometry. In International Journal of Heat and Mass Transfer, volume 40, No. 3, pages 533-544, 1997.

Y.-J. CHANG and C.-C. WANG:

Air Side Performance of Brazed Aluminium Heat Exchangers. In Journal of Enhanced Heat Transfer, volume 3, No. 1, pages 15-28, 1996.

R.-M. Manglik, A.-E. Bergles:

Heat Transfer and Pressure Drop Correlations for the Rectangular Offset Strip Fin Compact Heat Exchanger. In Experimental Thermal and Fluid Science, volume 10, pages 171-180, 1995.

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.HeatTransfer.HeatExchanger.kc_roundTube

Calculation of the mean convective heat transfer coefficient kc for the air-side heat transfer of heat exchangers with round tubes and several fin geometries.

Functions kc_roundTube and kc_roundTube_KC

There are basically three differences:

• The function kc_roundTube is using kc_roundTube_KC but offers additional output variables like e.g. Reynolds number or Nusselt number and failure status (an output of 1 means that the function is not valid for the inputs).
• Generally the function kc_roundTube_KC is numerically best used for the calculation of the mean convective heat transfer coefficient kc at known mass flow rate.
• You can perform an inverse calculation from kc_roundTube_KC, where an unknown mass flow rate is calculated out of a given mean convective heat transfer coefficient kc

Restriction

• According to the kind of fin geometry the calculation is valid in a range of Re from 300 to 8000.
• medium = air

Geometry

Calculation

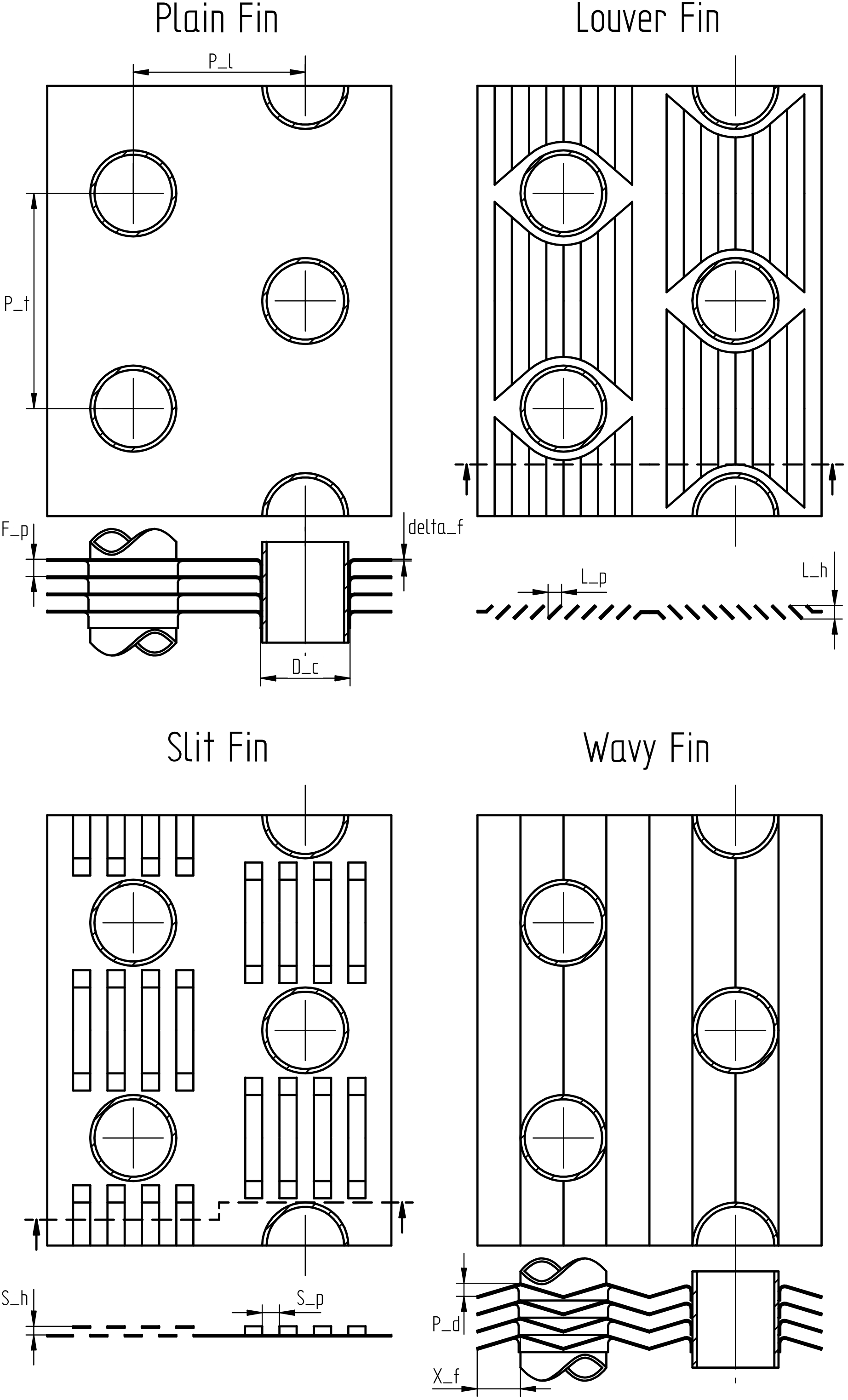
The mean convective heat transfer coefficient kc for heat exchanger is calculated through the corresponding Coulburn factor j:

j = f(geometry, Re)

with the resulting mean convective heat transfer coefficient kc

kc =  j * Re * Pr^(1/3) * lambda / D_c

with

Verification

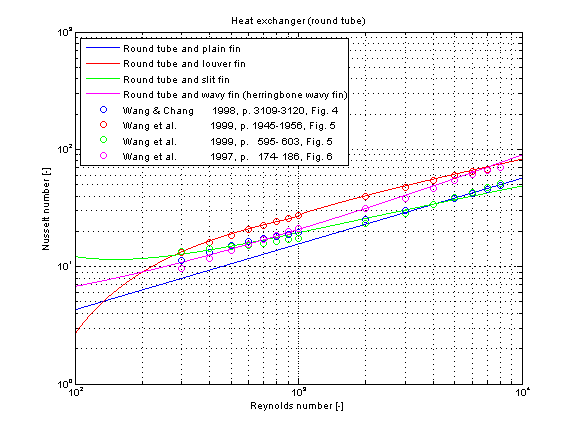
The mean Nusselt number Nu representing the mean convective heat transfer coefficient kc is shown below for different fin geometries at similar dimensions.

References

C.-C. Wang, C.-T. Chang:

Heat and mass transfer for plate fin-and-tube heat exchangers, with and without hydrophilic coating. In International Journal of Heat and Mass Transfer, volume 41, pages 3109-3120, 1998.

C.-C. Wang, C.-J. Lee, C.-T. Chang, S.-P. Lina:

Heat transfer and friction correlation for compact louvered fin-and-tube heat exchangers. In International Journal of Heat and Mass Transfer, volume 42, pages 1945-1956, 1999.

C.-C. Wang, W.-H. Tao, C.-J. Chang:

An investigation of the airside performance of the slit fin-and-tube heat exchangers. In International Journal of Refrigeration, volume 22, pages 595-603, 1999.

C.-C. Wang, W.-L. Fu, C.-T. Chang:

Heat Transfer and Friction Characteristics of Typical Wavy Fin-and-Tube Heat Exchangers. In Experimental Thermal and Fluid Science, volume 14, pages 174-186, 1997.

Extends from Modelica.Icons.Information (Icon for general information packages).