Modelica.Magnetic.FluxTubes.Examples.BasicExamples

Educational examples

Information

Extends from Modelica.Icons.ExamplesPackage (Icon for packages containing runnable examples).

Package Content

Name	Description
QuadraticCoreAirgap	Educational example: iron core with airgap
ToroidalCoreAirgap	Educational example: iron core with airgap
ToroidalCoreQuadraticCrossSection	Educational example: iron core with airgap
SaturatedInductor	Inductor with saturation in the ferromagnetic core

Modelica.Magnetic.FluxTubes.Examples.BasicExamples.QuadraticCoreAirgap

Educational example: iron core with airgap

Information

Educational example of a magnetic circuit containing an iron core and an airgap:

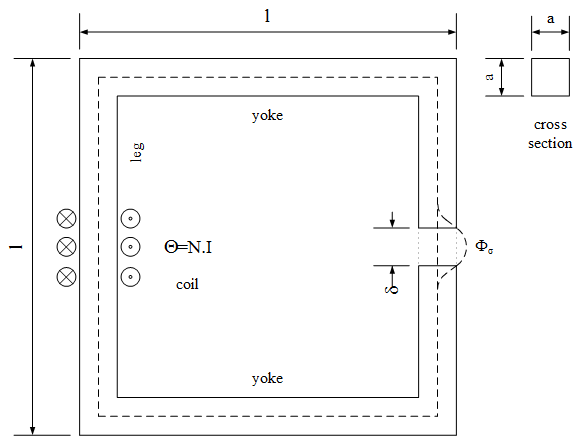
Magnetic circuit with iron core and airgap

A current ramp is applied in positive electric direction through the exciting coil, causing a rising magnetomotive force (mmf) in positive magnetic direction of the electromagnetic converter. The mmf in turn causes a magnetic flux through the circuit in the direction indicated by the flux sensor. From that magnetic flux, flux density can be calculated in every element of the magnetic circuit. Flux density is used to derive magnetic field strength. Magnetic field strength times length of the flux line gives magnetic potential difference of each element. The sum of all magnetic potential differences is covered by the mmf of the exciting coil.

Using the parameter values, the results can be validated by analytic calculations:

element	cross section	length	rel. permeability	B	H	mmf
left leg	a*a	l - a	μ_r	flux / cross section	B/(μ_r*μ₀)	H*length
upper yoke	a*a	l - a	μ_r	flux / cross section	B/(μ_r*μ₀)	H*length
right leg	a*a	l - a - delta	μ_r	flux / cross section	B/(μ_r*μ₀)	H*length
airgap	a*a	delta	1	useful flux / cross section	B/μ₀	H*length
lower yoke	a*a	l - a	μ_r	flux / cross section	B/(μ_r*μ₀)	H*length
total						Σ mmf = N*I

Note that there is a leakage flux path present. Therefore the total magnetic flux of in core splits into

the useful flux through the airgap and
the leakage flux through the leakage element.

However, the magnetic voltage across the airgap and the leakage model are equal. The ratio of the useful flux over the flux in the core is equal to 1 - σ. In the core the magnetic flux is the same in every element as they are connected in series. For the calculation of the length of flux lines inside the core, a medium flux line (dashed line) is used.

Additionally, a measuring coil is placed in the airgap. Due to Faraday's law, the time derivative of flux causes an induced voltage both in the exciting coil (in positive direction) and in the measuring coil (in negative direction). Since current and therefore flux are a linear time dependent ramp, induced voltages are constant during that ramp and zero otherwise. Note that usage of nonlinear magnetic material would change that result due the nonlinear relationship between magnetic field strength and flux density.

Note the proper usage of electric and magnetic grounds to define zero potential.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

Name	Description
l	Outer length of iron core [m]
a	Side length of square cross section [m]
mu_r	Relative permeability of core
delta	Length of airgap [m]
sigma	Leakage coefficient
N	Number of turns of exciting coil
I	Maximum exciting current [A]

Modelica.Magnetic.FluxTubes.Examples.BasicExamples.ToroidalCoreAirgap

Educational example: iron core with airgap

Information

Educational example of a magnetic circuit containing a toroidal iron core with circular cross section and an airgap:

Using the values shown in section Parameters, the results can be validated easily by analytic calculations:

element	cross section	length	rel. permeability	B	H	mmf
core	d²*pi/4	r*alpha	μ_r	flux / cross section	B/(μ_r*μ₀)	H*length
airgap	d²*pi/4	delta=r(2pi-alpha)	1	flux / cross section	B/(μ₀)	H*delta
total						Σ mmf = N*I

Note that since no leakage is present, the magnetic flux is the same in every element - they are connected in series. For calculation of the length of flux lines, a flux line in the middle of the toroid is used.

Additionally, a measuring coil is placed in the airgap. Due to Faraday's law, the time derivative of flux causes an induced voltage both in the exciting coil (in positive direction) and in the measuring coil (in negative direction). Since current is given as a linear-time dependent ramp, the induced voltages during that ramp are constant and otherwise zero. Note that usage of nonlinear magnetic material would change that result due the nonlinear relationship between magnetic field strength and flux density.

Note the proper usage of electric and magnetic grounds to define zero potential.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

Name	Description
r	Middle radius of iron core [m]
d	Diameter of cylindrical cross section [m]
mu_r	Relative permeability of core [1]
delta	Length of airgap [m]
alpha	Section angle of toroidal core [rad]
N	Number of exciting coil turns
I	Maximum exciting current [A]

Modelica.Magnetic.FluxTubes.Examples.BasicExamples.ToroidalCoreQuadraticCrossSection

Educational example: iron core with airgap

Information

Educational example of a magnetic circuit containing a toroidal iron core with rectangular cross section and an airgap:

Using the values shown in section Parameters, the results can be validated easily by analytic calculations:

element	cross section	length	rel. permeability	B	H	mmf
core	(r_o - r_i)*l	(r_o + r_i)/2*alpha	μ_r	flux / cross section	B/(μ_r*μ₀)	H*length
airgap	(r_o - r_i)*l	delta=(r_o + r_i)/2(2pi-alpha)	1	flux / cross section	B/(μ₀)	H*delta
total						Σ mmf = N*I

Note that since no leakage is present, the magnetic flux is the same in every element - they are connected in series. For calculation of the length of flux lines, a medium flux line is used.

Note the proper usage of electric and magnetic grounds to define zero potential.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Parameters

Name	Description
r_o	Outer radius of iron core [m]
r_i	Inner radius of iron core [m]
l	Length of rectangular cross section [m]
mu_r	Relative permeability of core [1]
delta	Length of airgap [m]
alpha	Section angle of toroidal core [rad]
N	Number of exciting coil turns
I	Maximum exciting current [A]

Modelica.Magnetic.FluxTubes.Examples.BasicExamples.SaturatedInductor

Inductor with saturation in the ferromagnetic core

Information

This model demonstrates the effects of non-linear magnetisation characteristics of soft magnetic materials (hysteresis neglected). A sinusoidal voltage is applied to an inductor with a closed ferromagnetic core of rectangular shape. Set the tolerance to 1e-7, simulate for 0.1 s and plot for example:

coil.i vs. time           // non-harmonic current due to saturation of the core material
r_mFe.mu_r vs. r_mFe.B    // relative permeability vs. flux density inside core
r_mFe.B vs. r_mFe.H       // magnetisation curve B(H); hysteresis neglected

The magnetisation characteristics of the flux tube element representing the ferromagnetic core can easily be changed from simplified linear behaviour (nonLinearPermeability set to false and R_mFe.mu_rConst set to a positive value, preferably mu_rConst >> 1) to non-linear behaviour (e.g., selection of one of the electric sheets in Material.SoftMagnetic with nonLinearPermeability set to true). This enables for convenient initial design of magnetic circuits with linear material characteristics prior to simulation with non-linear behaviour.

Note

If the supply voltage has a zero-crossing when applied to the inductor at time t=0 (i.e., source.phase set to zero instead of π/2), then the inrush current that is typical for switching of inductive loads can be observed.

Extends from Modelica.Icons.Example (Icon for runnable examples).

Automatically generated Thu Oct 1 16:07:48 2020.