Modelica.Mechanics.MultiBody.UsersGuide.Tutorial

This tutorial provides an introduction into the MultiBody library.

1. Overview of MultiBody library summarizes the most important aspects.
2. A first example describes in detail all the steps to build a simple pendulum model.
3. Loop structures explains how to model kinematic loops, especially by analytically solving non-linear equations.
4. ConnectionOfLineForces explains how to connect line force components directly together.

Extends from Modelica.Icons.Information (Icon for general information packages).

Package Content

Name	Description
OverView	Overview of MultiBody library
FirstExample	A first example
LoopStructures	Loop structures
ConnectionOfLineForces	Connection of LineForces

Modelica.Mechanics.MultiBody.UsersGuide.Tutorial.OverView

Library MultiBody is a free Modelica package providing 3-dimensional mechanical components to model in a convenient way mechanical systems, such as robots, mechanisms, vehicles. A basic feature is that all components have animation information with appropriate default sizes and colors. A typical screenshot of the animation of a double pendulum is shown in the figure below, together with its schematic.

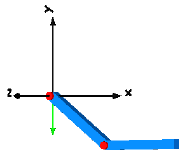
Note, that all components - the coordinate system of the world frame, the gravity acceleration vector, the revolute joints and the bodies - are visualized in the animation.
This library replaces the long available ModelicaAdditions.MultiBody library, since it is much more easier to use and more powerful. The main features of the library are:

• About 60 main components, i.e., joint, force, part, body, sensor and visualizer components that are ready to use and have useful default animation properties. One-dimensional force laws can be defined with components of the Modelica.Mechanics.Rotational and of the Modelica.Mechanics.Translational library and can be connected via available flange connectors to MultiBody components.
• About 75 functions to operate in a convenient way on orientation objects, e.g., to transform vector quantities between frames, or compute the orientation object of a planar rotation. The basic idea is to hide the actual definition of an orientation by providing essentially an Orientation type together with functions operating on instances of this type. Orientation objects based on a 3x3 transformation matrix and on quaternions are provided. As a side effect, the equations in all other components are simpler and easier to understand.
• A World model has to be present in every model on top level. Here the gravity field is defined (currently: no gravity, uniform gravity, point gravity), the visualization of the world coordinate system and default settings for animation. If a world model is not present, it is automatically provided together with a warning message.
• Built-in animation properties of all components, such as joints, forces, bodies, sensors. This allows an easy visual check of the constructed model. Animation of every component can be switched off via a parameter. The animation of a complete system can be switched off via one parameter in the world model. If animation is switched off, all equations related to animation are removed from the generated code. This is especially important for real-time simulation.
• Automatic handling of kinematic loops. Components can be connected together in a nearly arbitrary fashion. It does not matter whether components are flipped. This does not influence the efficiency. If kinematic loop structures occur, this is automatically handled in an efficient way by a new technique to transform a certain class of overdetermined sets of differential algebraic equations symbolically to a system where the number of equations and unknowns are the same (the user need not cut loops with special cut-joints to construct a tree-structure).
• Automatic state selection from joints and bodies. Most joints and all bodies have potential states. A Modelica translator will use the generalized coordinates of joints as states if possible. If this is not possible, states are selected from body coordinates. As a consequence, strange joints with 6 degrees of freedom are not necessary to define a body moving freely in space. An advanced user may select states manually from the Advanced menu of the corresponding components or use a Modelica parameter modification to set the "stateSelect" attribute directly.
• Analytic solution of kinematic loops. The non-linear equations occurring in kinematic loops are solved analytically for a large class of mechanisms, such as a 4 bar mechanism, a slider-crank mechanism or a MacPherson suspension. This is performed by constructing such loops with assembly joints JointXXX, available in the Modelica.Mechanics.MultiBody.Joints package. Assembly joints consist of 3 joints that have together 6 degrees of freedom, i.e., no constraints.They do not have potential states. When the motion of the two frame connectors are provided, a non-linear system of equation is solved analytically to compute the motion of the 3 joints. Analytic loop handling is especially important for real-time simulation.
• Line force components may have mass. Masses of line force components are located on the line on which the force is acting. They approximate the mass properties of a real physical device by one or two point masses. For example, a spring has often significant mass that has to be taken into account. If masses are set to zero, the additional code to handle these point masses is removed. If the masses are taken into account, the calculation overhead is small (the reason is that the occurring kinematic loops are analytically solved).
• Force components may be connected directly together, e.g., 3-dimensional springs in series connection. Usually, multi-body programs have the restriction that force components can only be connected between two bodies. Such restrictions are not present in the Modelica multi-body library, since it is a fully object-oriented, equation based library. Usually, if force components are connected directly together, non-linear systems of equations occur. The advantage is often, that this may avoid stiff systems that would occur if a small mass has to be put in between the two force elements.
• Initialization definition is available via menus. Initialization of states in joints and bodies can be performed in the parameter menu, without typing Modelica statements. For non-standard initialization, the usual Modelica commands can be used.
• Multi-body specific error messages. Annotations and assert statements have been introduced that provide in many cases warning or error messages that are related to the library components (and not to specific equations as it is usual in Modelica libraries). This requires appropriate tool support, as it is.
• Inverse models of mechanical systems can be easily defined by using motion generators, e.g., Modelica.Mechanics.Rotational.Position. Also, non-standard inverse models can be generated, e.g., when elasticity is present it might be necessary to differentiate equations several times.

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Mechanics.MultiBody.UsersGuide.Tutorial.FirstExample

As a first example it shall be demonstrated how to build up, simulate and animate a simple pendulum.

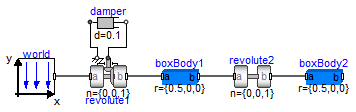
A simple pendulum consisting of a body and a revolute joint with linear damping in the joint, is first build-up as Modelica composition diagram, resulting in:

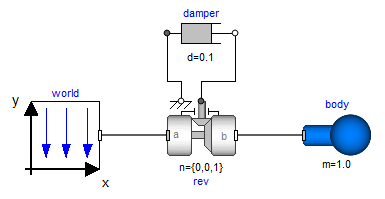
In the following figure the location of the used model components is shown. Drag these components in the diagram layer and connect them according to the figure:

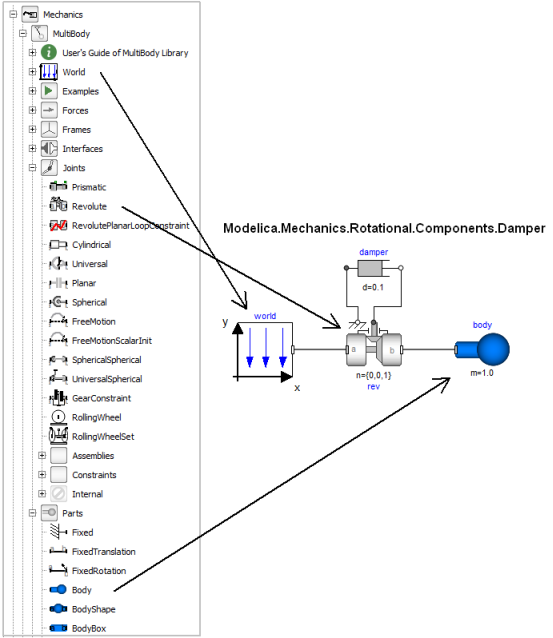
Every model that uses model components from the MultiBody library must have an instance of the Modelica.Mechanics.MultiBody.World model on highest level. The reason is that in the world object the gravity field is defined (uniform gravity or point gravity), as well as the default sizes of animation shapes and this information is reported to all used components. If the World object is missing, a warning message is printed and an instance of the World object with default settings is automatically utilized (this feature is defined with annotations).

In a second step the parameters of the dragged components need to be defined. Some parameters are vectors that have to be defined with respect to a local coordinate system of the corresponding component. The easiest way to perform this is to define a reference configuration of your multi-body model: In this configuration, the relative coordinates of all joints are zero. This means that all coordinate systems on all components are parallel to each other. Therefore, this just means that all vectors are resolved in the world frame in this configuration.

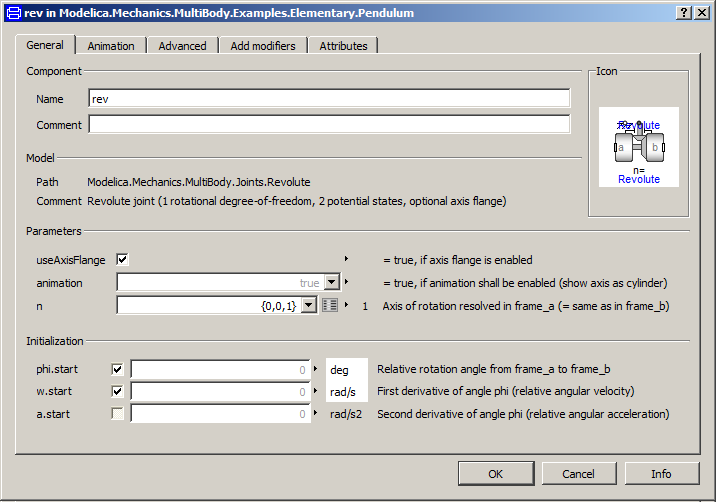
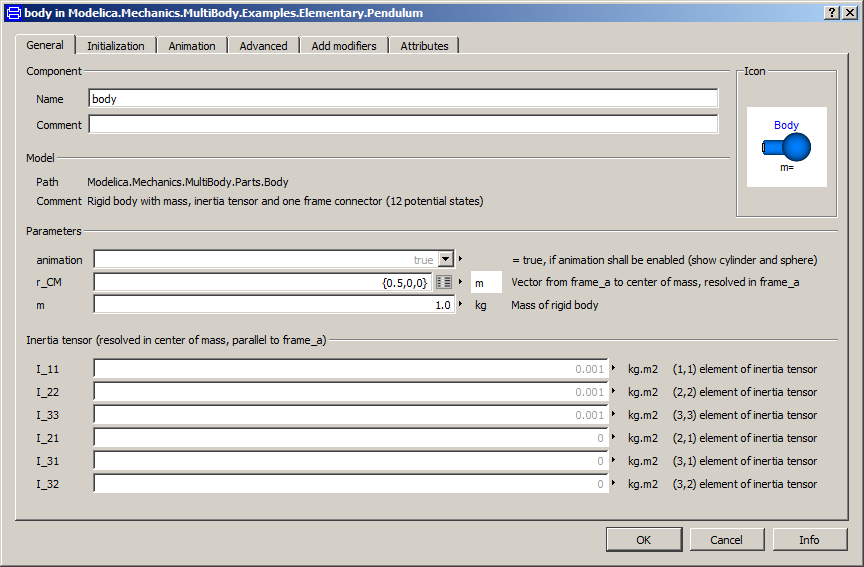
The reference configuration for the simple pendulum shall be defined in the following way: The y-axis of the world frame is directed upwards, i.e., the opposite direction of the gravity acceleration. The x-axis of the world frame is orthogonal to it. The revolute joint is placed in the origin of the world frame. The rotation axis of the revolute joint is directed along the z-axis of the world frame. The body is placed on the x-axis of the world frame (i.e., the rotation angle of the revolute joint is zero, when the body is on the x-axis). In the following figures the definition of this reference configuration is shown in the parameter menus of the revolute joint and the body:

Translate and simulate the model. Automatically, all defined components are visualized in an animation using default absolute or relative sizes of the components. For example, a body is visualized as a sphere and as a cylinder. The default size of the sphere is defined as parameter in the world object. You may change this size in the "Animation" parameter menu of the body (see parameter menu above). The default size of the cylinder is defined relatively to the size of the sphere (half of the sphere size). With default settings, the following animation is defined:

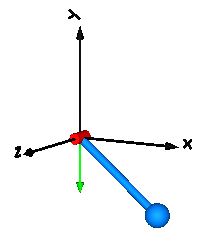
The world coordinate system is visualized as coordinate system with axes labels. The direction of the gravity acceleration vector is shown as green arrow. The red cylinder represents the rotation axis of the revolute joint and the light blue shapes represent the body. The center of mass of the body is in the middle of the light blue sphere.

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Mechanics.MultiBody.UsersGuide.Tutorial.ConnectionOfLineForces

Line force elements, such as a Spring, are usually connected between two parts. In fact, this is the only possibility in most multi-body programs. In an equation based system like Modelica, more general connections are possible. In particular 3-dimensional line force elements can be connected together in series without having a body with mass at the connection point. This is advantageous since stiff systems can be avoided, say, due to a stiff spring and a small mass at the connection point. For an example, see model ThreeSprings:

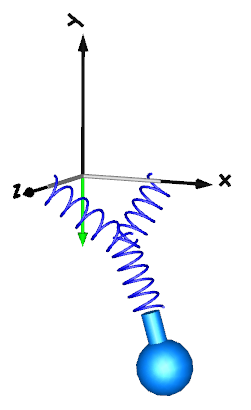
Here, three springs are connected together at one point, without having a body at the connection point of the springs. There is one difficulty: In such a situation the orientation object at the connection point is undefined, because the springs do not transmit torques. Translation will therefore fail, if three springs and a body are connected together in this way. To handle such a case, all line force elements have flags "fixedRotationAtFrame_a" and "fixedRotationAtFrame_b" in their "Advanced" parameter menu. For example, if "fixedRotationAtFrame_b = true", the orientation object at frame_b is explicitly set to a null rotation, i.e.,

frame_b.R = Modelica.Mechanics.MultiBody.Frames.nullRotation();

This means that the coordinate system in the connection point of the three springs is always parallel to the world frame. When this option is selected, the corresponding frame in the line force icon is marked with a red circle and with the text "R=0". This is shown in the next figure, where this option is selected for spring3.frame_b:

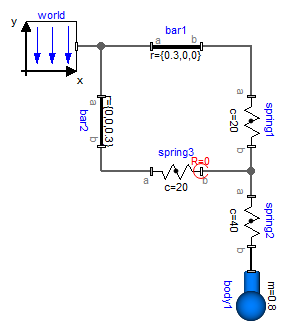
Note, if this flag is not set to true, a translation error will occur. Due to the usage of overdetermined connectors in the MultiBody library, the error message will be something like:

"The overdetermined connectors <…> are connected but do not have any root defined"

The two flags "fixedRotationAtFrame_a" and "fixedRotationAtFrame_b must be set very carefully because a wrong definition can lead to a model that simulates, but the simulation result is wrong. This is the case whenever the movement of the resulting system depends on the orientation object that was arbitrarily set in parallel to the world frame. A typical example is shown in the next figure:

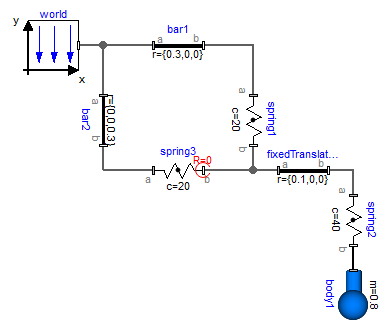
Here, spring3.frame_b.R is defined to be in parallel to the world frame. However, this is then also the orientation of fixedTranslation.frame_a, and this in turn means that the left part of the fixedTranslation object is always in parallel to the world frame. Since this is not correct, this model will result in a wrong simulation result This system is mathematically not well-defined and does not have a solution. The only way to model such a system is by providing a mass and an inertia tensor to fixedTranslation. Then, the flags are not needed, because the "connection" point of the springs is a body where the absolution position vector and the orientation matrix of the body-fixed coordinate system are used as states.

Extends from Modelica.Icons.Information (Icon for general information packages).