Modelica.Media.UsersGuide.MediumUsage

Content:

1. Basic usage of medium model
2. Medium model for a balance volume
3. Medium model for a pressure loss
4. Optional medium properties
5. Constants provided by medium model
6. Two-phase media
7. Initialization

A good demonstration how to use the media from Modelica.Media is given in package ModelicaTest.Media.TestsWithFluid. Under Modelica.Media.Examples.Utilities the most basic components of a Fluid library are defined. Additional media models with some very simple piping networks can be found in the ModelicaTest library under ModelicaTest.Media.TestsWithFluid.MediaTestModels.

Extends from Modelica.Icons.Information (Icon for general information packages).

Package Content

Name	Description
BasicUsage	Basic usage
BalanceVolume	Balance volume
ShortPipe	Short pipe
OptionalProperties	Optional properties
Constants	Constants
TwoPhase	Two-phase media
Initialization	Initialization

Modelica.Media.UsersGuide.MediumUsage.BasicUsage

Basic usage of medium model

Media models in Modelica.Media are provided by packages, inheriting from the partial package Modelica.Media.Interfaces.PartialMedium. Every package defines:

• Medium constants (such as the number of chemical substances, molecular data, critical properties, etc.).
• A BaseProperties model, to compute the basic thermodynamic properties of the fluid;
• setState_XXX functions to compute the thermodynamic state record from different input arguments (such as density, temperature, and composition which would be setState_dTX);
• Functions to compute additional properties (such as saturation properties, viscosity, thermal conductivity, etc.).

There are - as stated above - two different basic ways of using the Media library which will be described in more details in the following section. One way is to use the model BaseProperties. Every instance of BaseProperties for any medium model provides 3+nXi equations for the following 5+nXi variables that are declared in the medium model (nXi is the number of independent mass fractions, see explanation below):

Two variables out of p, d, h, or u, as well as the mass fractions Xi are the independent variables and the medium model basically provides equations to compute the remaining variables, including the full mass fraction vector X (more details to Xi and X are given further below).

In a component, the most basic usage of a medium model is as follows

model Pump
  replaceable package Medium = Modelica.Media.Interfaces.PartialMedium
                       "Medium model" annotation (choicesAllMatching = true);
  Medium.BaseProperties medium_a "Medium properties at location a (e.g., port_a)";
  // Use medium variables (medium_a.p, medium_a.T, medium_a.h, ...)
   ...
end Pump;

The second way is to use the setState_XXX functions to compute the thermodynamic state record from which all other thermodynamic state variables can be computed (see Basic definition of medium for further details on ThermodynamicState). The setState_XXX functions accept either X or Xi (see explanation below) and will decide internally which of these two compositions is provided by the user. The four fundamental setState_XXX functions are provided in PartialMedium

The simple example that explained the basic usage of BaseProperties would then become

model Pump
  replaceable package Medium = Modelica.Media.Interfaces.PartialMedium
                       "Medium model" annotation (choicesAllMatching = true);
  Medium.ThermodynamicState state_a "Thermodynamic state record at location a (e.g., port_a)";
  // Compute medium variables from thermodynamic state record (pressure(state_a), temperature(state_a),
  // specificEnthalpy(state_a), ...)
  ...
end Pump;

All media models are directly or indirectly a subpackage of package Modelica.Media.Interfaces.PartialMedium. Therefore, a medium model in a component should inherit from this partial package. Via the annotation "choicesAllMatching = true" it is defined that the tool should display a selection box with all loaded packages that inherit from PartialMedium. An example is given in the next figure:

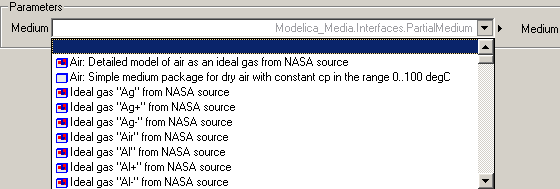
A selected medium model leads, e.g., to the following equation:

Pump pump(redeclare package Medium = Modelica.Media.Water.SimpleLiquidWater);

Usually, a medium model is associated with the variables of a fluid connector. Therefore, equations have to be defined in a model that relate the variables in the connector with the variables in the medium model:

model Pump
  replaceable package Medium = Modelica.Media.Interfaces.PartialMedium
                       "Medium model" annotation (choicesAllMatching = true);
  Medium.BaseProperties medium_a "Medium properties of port_a";
  // definition of the fluid port port_a
   ...
equation
  medium.p = port_a.p;
  medium.h = port_a.h;
  medium.Xi = port_a.Xi;
   ...
end Pump;

model Pump
  replaceable package Medium = Modelica.Media.Interfaces.PartialMedium
                       "Medium model" annotation (choicesAllMatching = true);
  Medium.ThermodynamicState state_a "Thermodynamic state record of medium at port_a";
  // definition of the fluid port port_a
   ...
equation
  state_a = Medium.setState_phX(port_a.p, port_a.h, port_a.Xi) // if port_a contains the variables
                                                               // p, h, and Xi
   ...
end Pump;

in the case of using ThermodynamicState.

If a component model shall treat both single and multiple substance fluids, equations for the mass fractions have to be present (above: medium.Xi = port_a.Xi) in the model. According to the Modelica semantics, the equations of the mass fractions are ignored, if the dimension of Xi is zero, i.e., for a single-component medium. Note, by specific techniques sketched in section "Medium definition", the independent variables in the medium model need not to be the same as the variables in the connector and still get the same efficiency, as if the same variables would be used.

If a fluid consists of a single substance, nXi = 0 and the vector of mass fractions Xi is not present. If a fluid consists of nS substances, the medium model may define the number of independent mass fractions nXi to be nS, nS-1, or zero. In all cases, balance equations for nXi substances have to be given in the corresponding component (see discussion below). Note, that if nXi = nS, the constraint "sum(Xi)=1" between the mass fractions is not present in the model; in that case, it is necessary to provide consistent start values for Xi such that sum(Xi) = 1.

The reason for this definition of Xi is that a fluid component library can be implemented by using only the independent mass fractions Xi and then via the medium it is defined how Xi is interpreted:

• If Xi = nS, then the constraint equation sum(X) = 1 is neglected during simulation. By making sure that the initial conditions of X fulfill this constraint, it can usually be guaranteed that small errors in sum(X) = 1 remain small although this constraint equation is not explicitly used during the simulation. This approach is usually useful if components of the mixture can become very small. If such a small quantity is computed via the equation 1 - sum(X[1:nX-1]), there might be large numerical errors and it is better to compute it via the corresponding balance equation.
• If Xi = nS-1, then the true independent mass fractions are used in the fluid component and the last component of X is computed via X[nX] = 1 - sum(Xi). This is useful for, e.g., MoistAir, where the number of states should be as small as possible without introducing numerical problems.
• If Xi = 0, then the reference value of composition reference_X is assumed. This case is useful to avoid composition states in all the cases when the composition will always be constant, e.g., with circuits having fixed composition sources.

The full vector of mass fractions X[nX] is computed in PartialMedium.BaseProperties based on Xi, reference_X, and the information whether Xi = nS or nS-1. For single-substance media, nX = 0, so there's also no X vector. For multiple-substance media, nX = nS, and X always contains the full vector of mass fractions. In order to reduce confusion for the user of a fluid component library, "Xi" has the annotation "HideResult=true", meaning, that this variable is not shown in the plot window. Only X is shown in the plot window and this vector always contains all mass fractions.

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Media.UsersGuide.MediumUsage.BalanceVolume

Fluid libraries usually have balance volume components with one fluid connector port that fulfill the mass and energy balance and on a different grid components that fulfill the momentum balance. A balance volume component, called junction volume below, should be primarily implemented in the following way (see also the implementation in Modelica.Media.Examples.Utilities.PortVolume):

model JunctionVolume
  import Modelica.Units.SI;
  import Modelica.Media.Examples.Utilities.FluidPort_a;

  parameter SI.Volume V = 1e-6 "Fixed size of junction volume";
  replaceable package Medium = Modelica.Media.Interfaces.PartialMedium
                         "Medium model" annotation (choicesAllMatching = true);

  FluidPort_a port(redeclare package Medium = Medium);
  Medium.BaseProperties medium(preferredMediumStates = true);

  SI.Energy U              "Internal energy of junction volume";
  SI.Mass   M              "Mass of junction volume";
  SI.Mass   MX[Medium.nXi] "Independent substance masses of junction volume";
equation
  medium.p   = port.p;
  medium.h   = port.h;
  medium.Xi = port.Xi;

  M  = V*medium.d;                  // mass of JunctionVolume
  MX = M*medium.Xi;                 // mass fractions in JunctionVolume
  U  = M*medium.u;                  // internal energy in JunctionVolume

  der(M)  = port.m_flow;    // mass balance
  der(MX) = port.mX_flow;   // substance mass balance
  der(U)  = port.H_flow;    // energy balance
end JunctionVolume;

Assume the Modelica.Media.Air.SimpleAir medium model is used with the JunctionVolume model above. This medium model uses pressure p and temperature T as independent variables. If the flag "preferredMediumStates" is set to true in the declaration of "medium", then the independent variables of this medium model get the attribute "stateSelect = StateSelect.prefer", i.e., the Modelica translator should use these variables as states, if this is possible. Basically, this means that constraints between the potential states p,T and the potential states U,M are present. A Modelica tool will therefore automatically differentiate medium equations and will use the following equations for code generation (note the equations related to X are removed, because SimpleAir consists of a single substance only):

M  = V*medium.d;
U  = M*medium.u;

// balance equations
der(M)  = port.m_flow;
der(U)  = port.H_flow;

// abbreviations introduced to get simpler terms
p = medium.p;
T = medium.T;
d = medium.d;
u = medium.u;
h = medium.h;

// medium equations
d = fd(p,T);
h = fh(p,T);
u = h - p/d;

// equations derived automatically by a Modelica tool due to index reduction
der(U) = der(M)*u + M*der(u);
der(M) = V*der(d);
der(u) = der(h) - der(p)/d - p/der(d);
der(d) = der(fd,p)*der(p) + der(fd,T)*der(T);
der(h) = der(fh,p)*der(p) + der(fd,T)*der(T);

Note, that "der(y,x)" is an operator that characterizes in the example above the partial derivative of y with respect to x (this operator will be included in one of the next Modelica language releases). All media models in this library are written in such a way that at least the partial derivatives of the medium variables with respect to the independent variables are provided, either because the equations are directly given (= symbolic differentiation is possible) or because the derivative of the corresponding function (such as fd above) is provided. A Modelica tool will transform the equations above in differential equations with p and T as states, i.e., will generate equations to compute der(p) and der(T) as function of p and T.

Note, when preferredMediumStates = false, no differentiation will take place and the Modelica translator will use the variables appearing differentiated as states, i.e., M and U. This has the disadvantage that for many media non-linear systems of equations are present to compute the intrinsic properties p, d, T, u, h from M and U.

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Media.UsersGuide.MediumUsage.ShortPipe

Fluid libraries have components with two ports that store neither mass nor energy and fulfill the momentum equation between their two ports, e.g., a short pipe. In most cases this means that an equation is present relating the pressure drop between the two ports and the mass flow rate from one to the other port. Since no mass or energy is stored, no differential equations for thermodynamic variables are present. A component model of this type has therefore usually the following structure (see also the implementation in Modelica.Media.Examples.Utilities.ShortPipe):

model ShortPipe
  import Modelica.Units.SI;
  import Modelica.Media.Examples.Utilities;

  // parameters defining the pressure drop equation

  replaceable package Medium = Modelica.Media.Interfaces.PartialMedium
                         "Medium model" annotation (choicesAllMatching = true);

  Utilities.FluidPort_a port_a (redeclare package Medium = Medium);
  Utilities.FluidPort_b port_b (redeclare package Medium = Medium);

  SI.Pressure dp = port_a.p - port_b.p "Pressure drop";
  Medium.BaseProperties medium_a "Medium properties in port_a";
  Medium.BaseProperties medium_b "Medium properties in port_b";
equation
  // define media models of the ports
  medium_a.p   = port_a.p;
  medium_a.h   = port_a.h;
  medium_a.Xi = port_a.Xi;

  medium_b.p   = port_b.p;
  medium_b.h   = port_b.h;
  medium_b.Xi = port_b.Xi;

  // Handle reverse and zero flow (semiLinear is a built-in Modelica operator)
  port_a.H_flow   = semiLinear(port_a.m_flow, port_a.h, port_b.h);
  port_a.mXi_flow = semiLinear(port_a.m_flow, port_a.Xi, port_b.Xi);

  // Energy, mass and substance mass balance
  port_a.H_flow + port_b.H_flow = 0;
  port_a.m_flow + port_b.m_flow = 0;
  port_a.mXi_flow + port_b.mXi_flow = zeros(Medium.nXi);

  // Provide equation: port_a.m_flow = f(dp)
end ShortPipe;

The semiLinear(..) operator is basically defined as:

semiLinear(m_flow, ha, hb) = if m_flow ≥ 0 then m_flow*ha else m_flow*hb;

that is, it computes the enthalpy flow rate either from the port_a or from the port_b properties, depending on flow direction. The exact details of this operator are given in ModelicaReference.Operators.'semiLinear()'. Especially, rules are defined in the Modelica specification that m_flow = 0 can be treated in a "meaningful way". Especially, if n fluid components (such as pipes) are connected together and the fluid connector from above is used, a linear system of equations appear between medium1.h, medium2.h, medium3.h, ..., port1.h, port2.h, port3.h, ..., port1.H_flow, port2.H_flow, port3.H_flow, .... The rules for the semiLinear(..) operator allow the following solution of this linear system of equations:

• n = 2 (two components are connected):
  The linear system of equations can be analytically solved with the result

  medium1.h = medium2.h = port1.h = port2.h
  0 = port1.H_flow + port2.H_flow
       

  Therefore, no problems with zero mass flow rate are present.
• n > 2 (more than two components are connected together):
  The linear system of equations is solved numerically during simulation. For m_flow = 0, the linear system becomes singular and has an infinite number of solutions. The simulator could use the solution t that is closest to the solution in the previous time step ("least squares solution"). Physically, the solution is determined by diffusion which is usually neglected. If diffusion is included, the linear system is regular.

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Media.UsersGuide.MediumUsage.OptionalProperties

In some cases additional medium properties are needed. A component that needs these optional properties has to call one of the functions listed in the following table. They are defined as partial functions within package PartialMedium, and then (optionally) implemented in actual medium packages. If a component calls such an optional function and the medium package does not provide a new implementation for this function, an error message is printed at translation time, since the function is "partial", i.e., incomplete. The argument of all functions is the state record, automatically defined by the BaseProperties model or specifically computed using the setState_XXX functions, which contains the minimum number of thermodynamic variables needed to compute all the additional properties. In the table it is assumed that there is a declaration of the form:

replaceable package Medium = Modelica.Media.Interfaces.PartialMedium;
Medium.ThermodynamicState state;

There are also some short forms provided for user convenience that allow the computation of certain thermodynamic state variables without using the ThermodynamicState record explicitly. Those short forms are for example useful to compute consistent start values in the initial equation section. Let's consider the function temperature_phX(p,h,X) as an example. This function computes the temperature from pressure, specific enthalpy, and composition X (or Xi) and is a short form for writing

temperature(setState_phX(p,h,X))

The following functions are predefined in PartialMedium (other functions can be added in the actual medium implementation package if they are useful)

Assume for example that the dynamic viscosity eta is needed in the pressure drop equation of a short pipe. Then, the model of a short pipe has to be changed to:

model ShortPipe
    ...
  Medium.BaseProperties medium_a "Medium properties in port_a";
  Medium.BaseProperties medium_b "Medium properties in port_b";
    ...
  Medium.DynamicViscosity eta;
    ...
  eta = if port_a.m_flow > 0 then
             Medium.dynamicViscosity(medium_a.state)
        else
             Medium.dynamicViscosity(medium_b.state);
  // use eta in the pressure drop equation: port_a.m_flow = f(dp, eta)
end ShortPipe;

Note, "Medium.DynamicViscosity" is a type defined in Modelica.Interfaces.PartialMedium as

import Modelica.Units.SI;
type DynamicViscosity = SI.DynamicViscosity (
                                   min=0,
                                   max=1.e8,
                                   nominal=1.e-3,
                                   start=1.e-3);

Every medium model may modify the attributes, to provide, e.g., min, max, nominal, and start values adapted to the medium. Also, other types, such as AbsolutePressure, Density, MassFlowRate, etc. are defined in PartialMedium. Whenever possible, these medium specific types should be used in a model in order that medium information, e.g., about nominal or start values, are automatically utilized.

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Media.UsersGuide.MediumUsage.Constants

Every medium model provides the following constants. For example, if a medium is declared as:

replaceable package Medium = Modelica.Media.Interfaces.PartialMedium;

then constants "Medium.mediumName", "Medium.nX", etc. are defined:

The record FluidConstants that is defined in PartialMedium contains the following elements

This record is extended in the partial packages further down the hierarchy (such as PartialTwoPhaseMedium or PartialMixtureMedium) and may contain some or all of the following elements

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Media.UsersGuide.MediumUsage.TwoPhase

Models for media which can exist in one-phase or two-phase conditions inherit from Modelica.Media.Interfaces.PartialTwoPhaseMedium (which inherits from PartialMedium). The basic usage of these media models is the same as described in the previous sections. However, additional functionalities are provided, which apply only to potentially two-phase media.

The following additional medium constants are provided:

The setState_ph(), setState_ps(), setState_dT() and setState_pT() functions have one extra input, named phase. If the phase input is not specified, or if it is given a value of zero, then the setState function will determine the phase, based on the other input values. An input phase = 1 will force the setState function to return a state vector corresponding to a one-phase state, while phase = 2 will force the setState value to return a state vector corresponding to a two-phase state, as shown in the following example;

  replaceable package Medium = Modelica.Media.Interfaces.PartialTwoPhaseMedium;
  Medium.ThermodynamicState state, state1, state2;
equation
  // Set the state, given the pressure and the specific enthalpy
  // the phase is determined by the (p, h) values, and can be retrieved
  // from the state record
  state = Medium.setState_ph(p, h);
  phase = state1.phase;

  // Force the computation of the state with one-phase
  // equations of state, irrespective of the (p, h) values
  state1 = Medium.setState_ph(p, h, 1);

  // Force the computation of the state with 2-phase
  // equations of state, irrespective of the (p, h) values
  state2 = Medium.setState_ph(p, h, 2);

This feature can be used for the following purposes:

• saving computational time, if one knows in advance the phase of the medium;
• unambiguously determine the phase, when the two inputs correspond to a point on the saturation boundary (the derivative functions have substantially different values on either side);
• get the properties of metastable states, like superheated water or subcooled vapour.

Many additional optional functions are defined to compute properties of saturated media, either liquid (bubble point) or vapour (dew point). The argument to such functions is a SaturationProperties record, which can be set starting from either the saturation pressure or the saturation temperature, as shown in the following example.

  replaceable package Medium = Modelica.Media.Interfaces.PartialTwoPhaseMedium;
  Medium.SaturationProperties sat_p;
  Medium.SaturationProperties sat_T;
equation
  // Set sat_p to saturation properties at pressure p
  sat_p = Medium.setSat_p(p);

  // Compute saturation properties at pressure p
  saturationTemperature_p = Medium.saturationTemperature_sat(sat_p);
  bubble_density_p =        Medium.bubbleDensity(sat_p);
  dew_enthalpy_p   =        Medium.dewEnthalpy(sat_p);

  // Set sat_T to saturation properties at temperature T
  sat_T = Medium.setSat_T(T);

  // Compute saturation properties at temperature T
  saturationTemperature_T = Medium.saturationPressure_sat(sat_T);
  bubble_density_T =        Medium.bubbleDensity(sat_T);
  dew_enthalpy_T =          Medium.dewEnthalpy(sat_T);

With reference to a model defining a pressure p, a temperature T, and a SaturationProperties record sat, the following functions are provided:

Sometimes it can be necessary to compute fluid properties in the thermodynamic plane, just inside or outside the saturation dome. In this case, it is possible to obtain an instance of a ThermodynamicState state vector, and then use it to call the additional functions already defined for one-phase media.

Here are some examples:

  replaceable package Medium = Modelica.Media.Interfaces.PartialTwoPhaseMedium;
  Medium.SaturationProperties sat;
  Medium.ThermodynamicState   dew_1;    // dew point, one-phase side
  Medium.ThermodynamicState   bubble_2; // bubble point, two phase side
equation
  // Set sat to saturation properties at pressure p
  sat = setSat_p(p);

  // Compute dew point properties, (default) one-phase side
  dew_1 = setDewState(sat);
  cpDew = Medium.specificHeatCapacityCp(dew_1);
  drho_dp_h_1 = Medium.density_derp_h(dew_1);

  // Compute bubble point properties, two-phase side
  bubble_2    = setBubbleState(sat, 2);
  drho_dp_h_2 = Medium.density_derp_h(bubble_2);

Extends from Modelica.Icons.Information (Icon for general information packages).

Modelica.Media.UsersGuide.MediumUsage.Initialization

When a medium model is used in a balance volume, differential equations for the independent medium variables are present and therefore initial conditions have to be provided. The following possibilities exist:

Steady state initialization

Modelica has currently no language element to define steady state initialization. In the Modelica simulation environment Dymola, the option

Advanced.DefaultSteadyStateInitialization = true

can be set before translation. Then, missing initial conditions are provided by automatically setting appropriate state derivatives to zero.

Explicit start values or initial equations

Explicit start values can be defined with the "start" and "fixed" attributes. The number of independent variables nx need to be known which can be deduced from the medium constants (nx = nXi + if singleState then 1 else 2). Then, start values or initial equations can be defined for nx variables (= p, T, d, u, h, Xi) from Medium.BaseProperties, e.g., in the form:

   replaceable package Medium = Medium.Interfaces.PartialMedium;
   Medium.BaseProperties medium1 (p(start=1e5, fixed=not Medium.singleState),
                                  T(start=300, fixed=true));
   Medium.BaseProperties medium2;
initial equation
   if not Medium.singleState then
      medium2.p = 1e5;
   end if;
   medium2.T = 300;
equation

If initial conditions are not provided for the independent medium variables, non-linear systems of equations may occur to compute the initial values of the independent medium variables from the provided initial conditions.

Guess values

If non-linear systems of equations occur during initialization, e.g., in case of steady state initialization, guess values for the iteration variables of the non-linear system of equations have to be provided via the "start" attribute (and fixed=false). Unfortunately, it is usually not known in advance which variables are selected as iteration variables of a non-linear system of equations. One of the following possibilities exist:

• Do not supply start values and hope that the medium specific types have meaningful start values, such as in "Medium.AbsolutePressure"
• Supply start values on all variables of the BaseProperties model, i.e., on p, T, d, u, h, Xi.
• Determine the iteration variables of the non-linear systems of equations and provide start values for these variables. In the Modelica simulation environment Dymola, the iteration variables can be determined by setting the command Advanced.OutputModelicaCode = true and by inspection of the file "dsmodel.mof" that is generated when this option is set (search for "nonlinear").

Extends from Modelica.Icons.Information (Icon for general information packages).