This information is part of the Modelica Standard Library maintained by the Modelica Association.

Calculation of the mean convective heat transfer coefficient kc for a hydrodynamically developed turbulent fluid flow over an even surface.

Functions kc_turbulent and kc_turbulent_KC

There are basically three differences:

• The function kc_turbulent is using kc_turbulent_KC but offers additional output variables like e.g. Reynolds number or Nusselt number and failure status (an output of 1 means that the function is not valid for the inputs).
• Generally the function kc_turbulent_KC is numerically best used for the calculation of the mean convective heat transfer coefficient kc at known mass flow rate.
• You can perform an inverse calculation from kc_turbulent_KC, where an unknown mass flow rate is calculated out of a given mean convective heat transfer coefficient kc

Restriction

• constant wall temperature
• turbulent regime (Reynolds number 5e5 < Re < 1e7)
• Prandtl number 0.6 ≤ Pr ≤ 2000

Geometry

Calculation

The mean convective heat transfer coefficient kc for flat plate is calculated through the corresponding Nusselt number Nu_turb according to [VDI 2002, p. Gd 1, eq. 2]:

Nu_turb = (0.037 * Re^0.8 * Pr) / (1 + 2.443/Re^0.1 * (Pr^(2/3)-1))

and the corresponding mean convective heat transfer coefficient kc:

kc =  Nu_turb * lambda / L

with

cp	as specific heat capacity at constant pressure [J/(kg.K)],
eta	as dynamic viscosity of fluid [Pa.s],
kc	as mean convective heat transfer coefficient [W/(m2.K)],
lambda	as heat conductivity of fluid [W/(m.K)],
L	as length of plate [m],
Nu_turb	as mean Nusselt number for turbulent regime [-],
Pr = eta*cp/lambda	as Prandtl number [-],
rho	as fluid density [kg/m3],
Re = v*rho*L/eta	as Reynolds number [-].

Verification

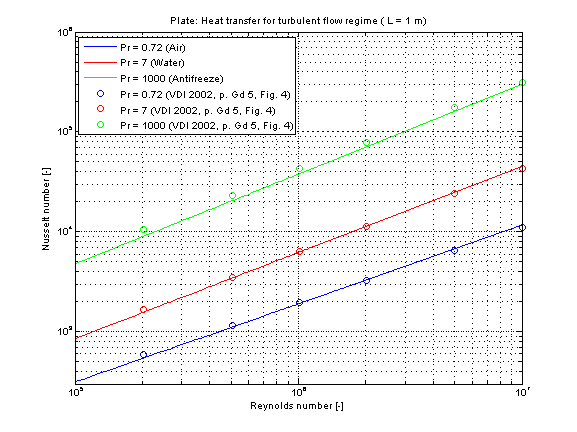
The mean Nusselt number in turbulent regime Nu representing the mean convective heat transfer coefficient kc for Prandtl numbers of different fluids is shown in the figure below.

References

VDI:

VDI - Wärmeatlas: Berechnungsblätter für den Wärmeübergang. Springer Verlag, 9th edition, 2002.