This information is part of the Modelica Standard Library maintained by the Modelica Association.

Approximates a function in a region between x0 and x1 such that

• The overall function is continuous with a continuous first derivative everywhere.
• The function is co-monotone with the given data points.

In this region, a continuation is constructed from the given points (x0, y0), (x1, y1) and the respective derivatives. For this purpose, a single polynomial of third order or two cubic polynomials with a linear section in between are used [Gasparo and Morandi, 1991]. This algorithm was extended with two additional conditions to avoid saddle points with zero/infinite derivative that lead to integrator step size reduction to zero.

This function was developed for pressure loss correlations properly addressing the static head on top of the established requirements for monotonicity and smoothness. In this case, the present function allows to implement the exact solution in the limit of x1-x0 -> 0 or y1-y0 -> 0.

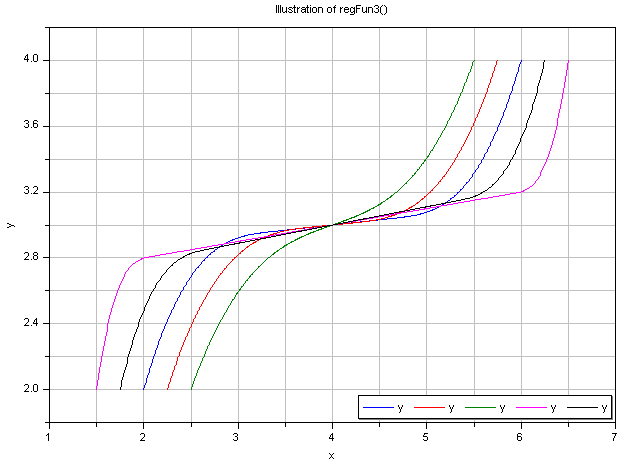
Typical screenshots for two different configurations are shown below. The first one illustrates five different settings of xi and yid:

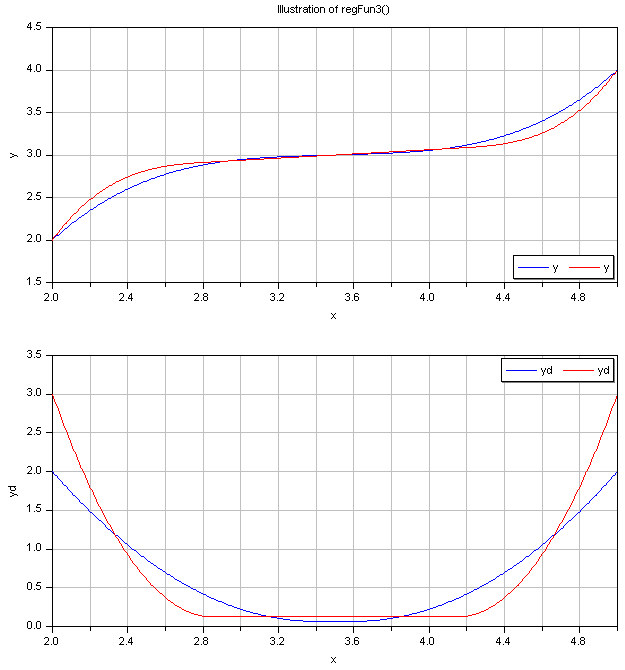
The second graph shows the continuous derivative of this regularization function:

Literature

Gasparo M. G. and Morandi R. (1991):

Piecewise cubic monotone interpolation with assigned slopes. Computing, Vol. 46, Issue 4, December 1991, pp. 355 - 365.

(y, c) = regFun3(x, x0, x1, y0, y1, y0d, y1d)

x	Type: Real Description: Abscissa value
x0	Type: Real Description: Lower abscissa value
x1	Type: Real Description: Upper abscissa value
y0	Type: Real Description: Ordinate value at lower abscissa value
y1	Type: Real Description: Ordinate value at upper abscissa value
y0d	Type: Real Description: Derivative at lower abscissa value
y1d	Type: Real Description: Derivative at upper abscissa value

y	Type: Real Description: Ordinate value
c	Type: Real Description: Slope of linear section between two cubic polynomials or dummy linear section slope if single cubic is used