.Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.HeatTransfer.StraightPipe.kc_twoPhaseOverall .Modelica.Fluid.Dissipation.Utilities.SharedDocumentation.HeatTransfer.StraightPipe.kc_twoPhaseOverallCalculation of local two phase heat transfer coefficient kc_2ph for (horizontal/vertical) boiling or (horizontal) condensation for an overall flow regime.
Boiling in a horizontal pipe (target = Modelica.Fluid.Dissipation.Utilities.Types.TwoPhaseHeatTransferTarget.BoilHor):
The local two phase heat transfer coefficient kc_2ph during boiling in a horizontal straight pipe for an overall regime is calculated according to [Gungor/Winterton 1986, p.354, eq. 2] :
kc_2ph = E_fc*E_fc_hor*kc_fc+S_nb+S_nb_hor*kc_nb
with
| Bo=qdot_A/(mdot_A*dh_lv) | as boiling number [-], |
| dh_lv | as evaporation enthalpy [J/kg], |
| E_fc=f(Bo,Fr_l,X_tt) | as forced convection enhancement factor [-], |
| E_fc_hor =f(Fr_l) | as forced convection enhancement factor for horizontal straight pipes [-], |
| Fr_l | as Froude number assuming total mass flow rate flowing as liquid [-], |
| kc_2ph | as local two phase heat transfer coefficient [W/(m2K)], |
| kc_fc | as heat transfer coefficient considering forced convection [W/(m2K)], |
| kc_nb | as heat transfer coefficient considering nucleate boiling [W/(m2K)], |
| mdot_A | as total mass flow rate density [kg/(m2s)], |
| qdot_A | as heat flow rate density [W/m2], |
| Re_l | as Reynolds number assuming liquid mass flow rate flowing alone [-], |
| S_nb =f(E_fc,Re_l) | as suppression factor of nucleate boiling [-], |
| S_nb_hor =f(Fr_l) | as suppression factor of nucleate boiling for horizontal straight pipes [-], |
| x_flow | as mass flow rate quality [-], |
| X_tt = f(x_flow) | as Martinelli parameter [-]. |
Boiling in a vertical pipe (target = Modelica.Fluid.Dissipation.Utilities.Types.TwoPhaseHeatTransferTarget.BoilVer):
The local two phase heat transfer coefficient kc_2ph during boiling in a vertical straight pipe for an overall regime is calculated out of the correlations for boiling in a horizontal straight pipe, where the horizontal correction factors E_fc_hor,S_nb_hor are unity.
Please note that the correlations named above are not valid for subcooled boiling due to a different driving temperature for nucleate boiling and forced convection. At subcooled boiling there is no enhancement factor (no vapour generation) but the suppression factor remains effective.
Condensation in a horizontal pipe (target = Modelica.Fluid.Dissipation.Utilities.Types.TwoPhaseHeatTransferTarget.CondHor):
The local two phase heat transfer coefficient kc_2ph during condensation in a horizontal straight pipe for an overall regime is calculated according to [Shah 1979, p.548, eq. 8] :
kc_2ph = kc_1ph*[(1 - x_flow)^0.8 + 3.8*x_flow^0.76*(1 - x_flow)^0.04/p_red^0.38]
where the convective heat transfer coefficient kc_1ph assuming the total mass flow rate is flowing as liquid according to [Shah 1979, p.548, eq. 5] :
kc_1ph = 0.023*Re_l^0.8*Pr_l^0.4*lambda_l/d_hyd
with
| d_hyd | as hydraulic diameter [m], |
| kc_2ph | as local two phase heat transfer coefficient [W/(m2K)], |
| kc_1ph | as convective heat transfer coefficient assuming total mass flow rate is flowing as liquid [W/(m2K)], |
| lambda_l | as thermal conductivity of fluid [W/(mK)], |
| pressure | as thermodynamic pressure of fluid [Pa], |
| p_crit | as critical pressure of fluid [Pa], |
| p_red = pressure/p_crit | as reduced pressure [-], |
| Pr_l | as Prandtl number assuming [-], |
| Re_l | as Reynolds number assuming total mass flow rate is flowing as liquid [-], |
| x_flow | as mass flow rate quality [-], |
The local two phase heat transfer coefficient kc_2ph during for horizontal and vertical boiling as well as for horizontal condensation is shown for a straight pipe in the figures below.
Boiling in a horizontal pipe (target = Modelica.Fluid.Dissipation.Utilities.Types.TwoPhaseHeatTransferTarget.BoilVer):
Here the validation of the two phase heat transfer coefficient is shown for boiling in a horizontal straight pipe.
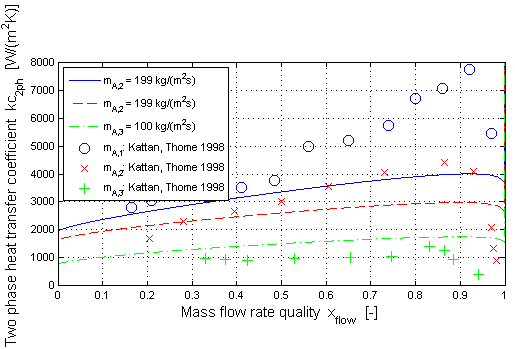
The two phase heat transfer coefficient (kc_2ph ) w.r.t. Gungor/Winterton is shown in dependence of the mass flow rate quality (x_flow ) for different mass flow rate densities (mdot_A ). The validation has been done with measurement results from Kattan/Thome for R134a as medium.
The two phase heat transfer coefficient increases with increasing mass flow rate quality up to a maximum value. After that there is a rapid decrease of (kc_2ph ) with increasing (x_flow ). This can be explained with a partial dryout of the pipe wall for a high mass flow rate quality.
Condensation in a horizontal pipe (target = Modelica.Fluid.Dissipation.Utilities.Types.TwoPhaseHeatTransferTarget.CondHor):
Here the validation of the two phase heat transfer coefficient is shown for condensation in a horizontal straight pipe.
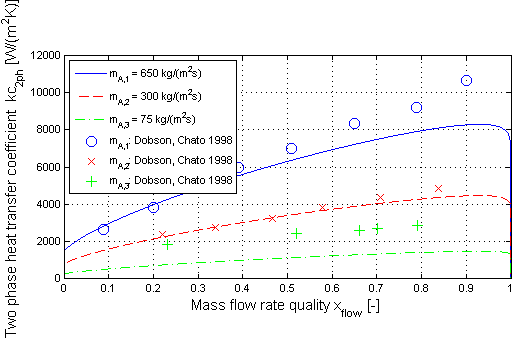
The two phase heat transfer coefficient (kc_2ph ) w.r.t. Shah is shown in dependence of the mass flow rate quality (x_flow ) for different mass flow rate densities (mdot_A ). The validation has been done with measurement results from Dobson/Chato for R134a as medium.