
This package hosts basic models for quasi stationary single phase circuits. Quasi stationary theory for single phase circuits can be found in the references.
Extends from Modelica.Icons.Package (Icon for standard packages).
| Name | Description |
|---|---|
Admittance | Single phase linear admittance |
Capacitor | Single phase linear capacitor |
Conductor | Single phase linear conductor |
Ground | Electrical ground |
Impedance | Single phase linear impedance |
Inductor | Single phase linear inductor |
Resistor | Single phase linear resistor |
VariableAdmittance | Single phase variable admittance |
VariableCapacitor | Single phase variable capacitor |
VariableConductor | Single phase variable conductor |
VariableImpedance | Single phase variable impedance |
VariableInductor | Single phase variable inductor |
VariableResistor | Single phase variable resistor |
Ground of a single phase circuit. The potential at the ground node is zero. Every electrical circuit, e.g., a series resonance example, has to contain at least one ground object.
| Type | Name | Description |
|---|---|---|
PositivePin | pin |
The linear resistor connects the complex voltage v with the complex
current i by i*R = v.
The resistance R is allowed to be positive, zero, or negative.
The resistor model also has an optional conditional heat port. A linear temperature dependency of the resistance is also taken into account.
Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.SinglePhase.Interfaces.OnePort (Two pins, current through) and Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Resistance | R_ref | Reference resistance at T_ref | |
Temperature | T_ref | 293.15 | Reference temperature |
LinearTemperatureCoefficient | alpha_ref | 0 | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) |
Boolean | useHeatPort | false | =true, if heatPort is enabled |
Temperature | T | T_ref | Fixed device temperature if useHeatPort = false |
| Type | Name | Description |
|---|---|---|
PositivePin | pin_p | Positive quasi-static single-phase pin |
NegativePin | pin_n | Negative quasi-static single-phase pin |
HeatPort_a | heatPort | Conditional heat port |
The linear conductor connects the voltage v with the
current i by i = v*G.
The conductance G is allowed to be positive, zero, or negative.
The conductor model also has an optional conditional heat port. A linear temperature dependency of the conductance is also taken into account.
Resistor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.SinglePhase.Interfaces.OnePort (Two pins, current through) and Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Conductance | G_ref | Reference conductance at T_ref | |
Temperature | T_ref | 293.15 | Reference temperature |
LinearTemperatureCoefficient | alpha_ref | 0 | Temperature coefficient of conductance (G_actual = G_ref/(1 + alpha_ref*(heatPort.T - T_ref)) |
Boolean | useHeatPort | false | =true, if heatPort is enabled |
Temperature | T | T_ref | Fixed device temperature if useHeatPort = false |
| Type | Name | Description |
|---|---|---|
PositivePin | pin_p | Positive quasi-static single-phase pin |
NegativePin | pin_n | Negative quasi-static single-phase pin |
HeatPort_a | heatPort | Conditional heat port |
The linear capacitor connects the voltage v with the
current i by i = j*ω*C*v.
The capacitance C is allowed to be positive, zero, or negative.
Resistor, Conductor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.SinglePhase.Interfaces.OnePort (Two pins, current through).
| Type | Name | Default | Description |
|---|---|---|---|
Capacitance | C | Capacitance |
| Type | Name | Description |
|---|---|---|
PositivePin | pin_p | Positive quasi-static single-phase pin |
NegativePin | pin_n | Negative quasi-static single-phase pin |
The linear inductor connects the voltage v with the
current i by v = j*ω*L*i.
The Inductance L is allowed to be positive, zero, or negative.
Resistor, Conductor, Capacitor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.SinglePhase.Interfaces.OnePort (Two pins, current through).
| Type | Name | Default | Description |
|---|---|---|---|
Inductance | L | Inductance |
| Type | Name | Description |
|---|---|---|
PositivePin | pin_p | Positive quasi-static single-phase pin |
NegativePin | pin_n | Negative quasi-static single-phase pin |
The impedance model represents a series connection of a resistor and either an inductor or capacitor.

The linear impedance connects the voltage v with the
current i by v = Z*i. The resistive
component is modeled temperature dependent, so the real part R_actual = real(Z) is determined from
the actual operating temperature and the reference input resistance real(Z_ref).
A conditional heat port is considered.
The reactive component X_actual = imag(Z)
is equal to imag(Z_ref) if frequencyDependent = false.
Frequency dependency is considered by frequencyDependent = true, distinguishing two cases:
imag(Z_ref) > 0: inductive caseX_actual is proportional to f/f_refimag(Z_ref) < 0: capacitive caseX_actual is proportional to f_ref/fResistor, Conductor, Capacitor, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.SinglePhase.Interfaces.OnePort (Two pins, current through) and Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
ComplexImpedance | Z_ref | Complex impedance R_ref + j*X_ref | |
Temperature | T_ref | 293.15 | Reference temperature |
LinearTemperatureCoefficient | alpha_ref | 0 | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) |
Boolean | useHeatPort | false | =true, if heatPort is enabled |
Temperature | T | T_ref | Fixed device temperature if useHeatPort = false |
Boolean | frequencyDependent | false | Consider frequency dependency, if true |
Frequency | f_ref | 1 | Reference frequency, if frequency dependency is considered |
final Resistance | R_ref | real(Z_ref) | Resistive component of impedance, resistance |
final Reactance | X_ref | imag(Z_ref) | Reactive component of impedance, reactance |
| Type | Name | Description |
|---|---|---|
PositivePin | pin_p | Positive quasi-static single-phase pin |
NegativePin | pin_n | Negative quasi-static single-phase pin |
HeatPort_a | heatPort | Conditional heat port |
The admittance model represents a parallel connection of a conductor and either a capacitor or inductor.
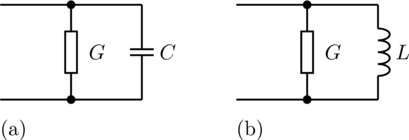
The linear admittance connects the voltage v with the
current i by i = Y*v. The resistive
component is modeled temperature dependent, so the real part G_actual = real(Y) is determined from
the actual operating temperature and the reference input conductance real(Y_ref).
A conditional heat port is considered.
The reactive component B_actual = imag(Y)
is equal to imag(Y_ref) if frequencyDependent = false.
Frequency dependency is considered by frequencyDependent = true, distinguishing two cases:
imag(Y_ref) > 0: capacitive caseB_actual is proportional to f/f_refimag(Y_ref) < 0: inductive caseB_actual is proportional to f_ref/fResistor, Conductor, Capacitor, Impedance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.SinglePhase.Interfaces.OnePort (Two pins, current through) and Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
ComplexAdmittance | Y_ref | Complex admittance G_ref + j*B_ref | |
Temperature | T_ref | 293.15 | Reference temperature |
LinearTemperatureCoefficient | alpha_ref | 0 | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) |
Boolean | useHeatPort | false | =true, if heatPort is enabled |
Temperature | T | T_ref | Fixed device temperature if useHeatPort = false |
Boolean | frequencyDependent | false | Consider frequency dependency, if true |
Frequency | f_ref | 1 | Reference frequency, if frequency dependency is considered |
final Conductance | G_ref | real(Y_ref) | Resistive component of conductance |
final Susceptance | B_ref | imag(Y_ref) | Reactive component of susceptance |
| Type | Name | Description |
|---|---|---|
PositivePin | pin_p | Positive quasi-static single-phase pin |
NegativePin | pin_n | Negative quasi-static single-phase pin |
HeatPort_a | heatPort | Conditional heat port |
The linear resistor connects the voltage v with the
current i by i*R = v.
The resistance R is given as input signal.
The variable resistor model also has an optional conditional heat port. A linear temperature dependency of the resistance is also taken into account.
A zero crossing of the R signal could cause singularities due to the actual structure of the connected network.
Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.SinglePhase.Interfaces.OnePort (Two pins, current through) and Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Temperature | T_ref | 293.15 | Reference temperature |
LinearTemperatureCoefficient | alpha_ref | 0 | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) |
Boolean | useHeatPort | false | =true, if heatPort is enabled |
Temperature | T | T_ref | Fixed device temperature if useHeatPort = false |
| Type | Name | Description |
|---|---|---|
PositivePin | pin_p | Positive quasi-static single-phase pin |
NegativePin | pin_n | Negative quasi-static single-phase pin |
HeatPort_a | heatPort | Conditional heat port |
input RealInput | R_ref | Variable resistance |
The linear conductor connects the voltage v with the
current i by i = G*v.
The conductance G is given as input signal.
The variable conductor model also has an optional conditional heat port. A linear temperature dependency of the conductance is also taken into account.
Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.SinglePhase.Interfaces.OnePort (Two pins, current through) and Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Temperature | T_ref | 293.15 | Reference temperature |
LinearTemperatureCoefficient | alpha_ref | 0 | Temperature coefficient of conductance (G_actual = G_ref/(1 + alpha_ref*(heatPort.T - T_ref)) |
Boolean | useHeatPort | false | =true, if heatPort is enabled |
Temperature | T | T_ref | Fixed device temperature if useHeatPort = false |
| Type | Name | Description |
|---|---|---|
PositivePin | pin_p | Positive quasi-static single-phase pin |
NegativePin | pin_n | Negative quasi-static single-phase pin |
HeatPort_a | heatPort | Conditional heat port |
input RealInput | G_ref | Variable conductance |
The linear capacitor connects the voltage v with the
current i by i = j*ω*C*v.
The capacitance C is given as input signal.
The abstraction of a variable capacitor at quasi stationary operation assumes:
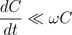 .
.
Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.SinglePhase.Interfaces.OnePort (Two pins, current through).
| Type | Name | Description |
|---|---|---|
PositivePin | pin_p | Positive quasi-static single-phase pin |
NegativePin | pin_n | Negative quasi-static single-phase pin |
input RealInput | C | Variable capacitances |
The linear inductor connects the branch voltage v with the
branch current i by v = j*ω*L*i. The inductance L is given as input signal.
The abstraction of a variable inductor at quasi stationary operation assumes:
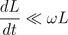
Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable impedance, Variable admittance,
Extends from Modelica.Electrical.QuasiStationary.SinglePhase.Interfaces.OnePort (Two pins, current through).
| Type | Name | Description |
|---|---|---|
PositivePin | pin_p | Positive quasi-static single-phase pin |
NegativePin | pin_n | Negative quasi-static single-phase pin |
input RealInput | L | Variable inductances |
The impedance model represents a series connection of a resistor and either an inductor or capacitor.

The linear impedance connects the complex voltage v with the
complex current i by i*Z = v.
The impedance Z_ref = R_ref + j*X_ref is given as complex input signal, representing the
resistive and reactive component of the input impedance. The resistive
component is modeled temperature dependent, so the real part R_actual = real(Z) is determined from
the actual operating temperature and the reference input resistance real(Z_ref).
The reactive component X_actual = imag(Z)
is equal to imag(Z_ref) if frequencyDependent = false.
Frequency dependency is considered by frequencyDependent = true, distinguishing two cases:
imag(Z_ref) > 0: inductive caseX_actual is proportional to f/f_refimag(Z_ref) < 0: capacitive caseX_actual is proportional to f_ref/f
A zero crossing of the real or imaginary part of the impedance signal Z_ref could cause
singularities due to the actual structure of the connected network.
Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.SinglePhase.Interfaces.OnePort (Two pins, current through) and Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Temperature | T_ref | 293.15 | Reference temperature |
LinearTemperatureCoefficient | alpha_ref | 0 | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) |
Boolean | useHeatPort | false | =true, if heatPort is enabled |
Temperature | T | T_ref | Fixed device temperature if useHeatPort = false |
Boolean | frequencyDependent | false | Consider frequency dependency, if true |
Frequency | f_ref | 1 | Reference frequency, if frequency dependency is considered |
| Type | Name | Description |
|---|---|---|
PositivePin | pin_p | Positive quasi-static single-phase pin |
NegativePin | pin_n | Negative quasi-static single-phase pin |
HeatPort_a | heatPort | Conditional heat port |
input ComplexInput | Z_ref | Variable complex impedance |
The admittance model represents a parallel connection of a conductor and either a capacitor or inductor.

The linear admittance connects the complex voltage v with the
complex current i by v*Y = i.
The admittance Y_ref = G_ref + j*B_ref is given as complex input signal, representing the
resistive and reactive component of the input admittance. The resistive
component is modeled temperature dependent, so the real part G_actual = real(Y) is determined from
the actual operating temperature and the reference input conductance real(Y_ref).
The reactive component B_actual = imag(Y)
is equal to imag(Y_ref) if frequencyDependent = false.
Frequency dependency is considered by frequencyDependent = true, distinguishing two cases:
imag(Y_ref) > 0: capacitive caseB_actual is proportional to f/f_refimag(Y_ref) < 0: inductive caseB_actual is proportional to f_ref/f
A zero crossing of the real or imaginary part of the admittance signal Y_ref could cause
singularities due to the actual structure of the connected network.
Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance
Extends from Modelica.Electrical.QuasiStationary.SinglePhase.Interfaces.OnePort (Two pins, current through) and Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Temperature | T_ref | 293.15 | Reference temperature |
LinearTemperatureCoefficient | alpha_ref | 0 | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) |
Boolean | useHeatPort | false | =true, if heatPort is enabled |
Temperature | T | T_ref | Fixed device temperature if useHeatPort = false |
Boolean | frequencyDependent | false | Consider frequency dependency, if true |
Frequency | f_ref | 1 | Reference frequency, if frequency dependency is considered |
| Type | Name | Description |
|---|---|---|
PositivePin | pin_p | Positive quasi-static single-phase pin |
NegativePin | pin_n | Negative quasi-static single-phase pin |
HeatPort_a | heatPort | Conditional heat port |
input ComplexInput | Y_ref | Variable complex admittance |
Generated 2018-12-12 12:10:23 EST by MapleSim.