
This package hosts basic models for quasi stationary multiphase circuits. Quasi stationary theory can be found in the references.
Extends from Modelica.Icons.Package (Icon for standard packages).
| Name | Description |
|---|---|
Admittance | Multiphase linear admittance |
Capacitor | Multiphase linear capacitor |
Conductor | Multiphase linear conductor |
Delta | Delta (polygon) connection |
Impedance | Multiphase linear impedance |
Inductor | Multiphase linear inductor |
MultiDelta | Delta (polygon) connection of multi phase systems consisting of multiple base systems |
MultiStar | Star connection of multi phase systems consisting of multiple base systems |
MultiStarResistance | Resistance connection of star points |
MutualInductor | Linear mutual inductor |
PlugToPin_n | Connect one (negative) pin |
PlugToPin_p | Connect one (positive) pin |
PlugToPins_n | Connect all (negative) pins |
PlugToPins_p | Connect all (positive) pins |
Resistor | Multiphase linear resistor |
Star | Star connection |
VariableAdmittance | Multiphase variable admittance |
VariableCapacitor | Multiphase variable capacitor |
VariableConductor | Multiphase variable conductor |
VariableImpedance | Multiphase variable impedance |
VariableInductor | Multiphase variable inductor |
VariableResistor | Multiphase variable resistor |
Star (wye) connection of a multi phase circuit. The potentials at the star points are the same.
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | |
NegativePin | pin_n |
Delta (polygon) connection of a multi phase circuit.
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | |
NegativePlug | plug_n |
Star (wye) connection of a multi phase circuit consisting of multiple base systems (see multi phase guidelines). The potentials at the star points are all equal.
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
final Integer | mSystems | Modelica.Electrical.MultiPhase.Functions.numberOfSymmetricBaseSystems(m) | Number of base systems |
final Integer | mBasic | integer(m / mSystems) | Phase number of base systems |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | |
NegativePlug | starpoints |
Delta (polygon) connection of a multi phase circuit consisting of multiple base systems (see multi phase guidelines).
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
final Integer | mSystems | Modelica.Electrical.MultiPhase.Functions.numberOfSymmetricBaseSystems(m) | Number of base systems |
final Integer | mBasic | integer(m / mSystems) | Phase number of base systems |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | |
NegativePlug | plug_n |
Multi star points are connected by resistors. This model is required to operate multi phase systems with even phase numbers to avoid ideal connections of start points of base systems; see multi phase guidelines.
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
final Integer | mBasic | Modelica.Electrical.MultiPhase.Functions.numberOfSymmetricBaseSystems(m) | Number of symmetric base systems |
Resistance | R | 1000000 | Insulation resistance between base systems |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug | |
NegativePin | pin |
Connects the single phase (positive) pin k of the multi phase (positive) plug to a single phase (positive) pin.
PlugToPin_n, PlutToPins_p, PlugToPins_n
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
Integer | k | 1 | Phase index |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | |
PositivePin | pin_p |
Connects the single phase (negative) pin k of the multi phase (negative) plug to a single phase (negative) pin.
PlugToPin_p, PlutToPins_p, PlugToPins_n
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
Integer | k | 1 | Phase index |
| Type | Name | Description |
|---|---|---|
NegativePlug | plug_n | |
NegativePin | pin_n |
Connects all m single phase (positive) pins of the multi phase (positive) plug to an array of m single phase (positive) pins.
PlugToPin_p, PlugToPin_n, PlugToPins_n
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | number of phases |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | |
PositivePin | pin_p[m] |
Connects all m single phase (negative) pins of the multi phase (negative) plug to an array of m single phase (negative) pins.
PlugToPin_p, PlugToPin_n, PlugToPins_p
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | number of phases |
| Type | Name | Description |
|---|---|---|
NegativePlug | plug_n | |
NegativePin | pin_n[m] |
The linear resistor connects the complex voltages v with the complex
currents i by i*R = v,
using m single phase Resistors.
The resistor model also has m optional
conditional heat ports.
A linear temperature dependency of the resistances for enabled heat ports is also taken into account.
Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.MultiPhase.Interfaces.TwoPlug (Two plugs with pin-adapter) and Modelica.Electrical.MultiPhase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
Resistance | R_ref[m] | Reference resistances at T_ref | |
Temperature | T_ref[m] | fill(293.15, m) | Reference temperatures |
LinearTemperatureCoefficient | alpha_ref[m] | zeros(m) | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) |
final Integer | mh | m | Number of heatPorts=number of phases |
Boolean | useHeatPort | false | =true, if all heat ports are enabled |
Temperature | T[mh] | T_ref | Fixed device temperatures if useHeatPort = false |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | Positive quasi-static polyphase plug |
NegativePlug | plug_n | Negative quasi-static polyphase plug |
HeatPort_a | heatPort[mh] | Conditional heat ports |
The linear resistor connects the complex currents i with the complex
voltages v by v*G = i,
using m single phase Conductors.
The conductor model also has m optional
conditional heat ports.
A linear temperature dependency of the conductances for enabled heat ports is also taken into account.
Conductor, Resistor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.MultiPhase.Interfaces.TwoPlug (Two plugs with pin-adapter) and Modelica.Electrical.MultiPhase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
Conductance | G_ref[m] | Reference conductances at T_ref | |
Temperature | T_ref[m] | fill(293.15, m) | Reference temperatures |
LinearTemperatureCoefficient | alpha_ref[m] | zeros(m) | Temperature coefficient of conductance (G_actual = G_ref/(1 + alpha_ref*(heatPort.T - T_ref)) |
final Integer | mh | m | Number of heatPorts=number of phases |
Boolean | useHeatPort | false | =true, if all heat ports are enabled |
Temperature | T[mh] | T_ref | Fixed device temperatures if useHeatPort = false |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | Positive quasi-static polyphase plug |
NegativePlug | plug_n | Negative quasi-static polyphase plug |
HeatPort_a | heatPort[mh] | Conditional heat ports |
The linear capacitor connects the complex currents i with the complex
voltages v by v*j*ω*C = i,
using m single phase Capacitors.
Capacitor, Resistor, Conductor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.MultiPhase.Interfaces.TwoPlug (Two plugs with pin-adapter).
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
Capacitance | C[m] | Capacitances |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | Positive quasi-static polyphase plug |
NegativePlug | plug_n | Negative quasi-static polyphase plug |
The linear inductor connects the complex voltages v with the complex
currents i by i*j*ω*L = v,
using m single phase Inductors.
Inductor, Resistor, Conductor, Capacitor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.MultiPhase.Interfaces.TwoPlug (Two plugs with pin-adapter).
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
Inductance | L[m] | Inductances |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | Positive quasi-static polyphase plug |
NegativePlug | plug_n | Negative quasi-static polyphase plug |
Model of a multi phase inductor providing a mutual inductance matrix model.
v[1] = j*omega*L[1,1]*i[1] + j*omega*L[1,2]*i[2] + ... + j*omega*L[1,m]*i[m]
v[2] = j*omega*L[2,1]*i[1] + j*omega*L[2,2]*i[2] + ... + j*omega*L[2,m]*i[m]
: : : :
v[m] = j*omega*L[m,1]*i[1] + j*omega*L[m,2]*i[2] + ... + j*omega*L[m,m]*i[m]
Extends from Modelica.Electrical.QuasiStationary.MultiPhase.Interfaces.OnePort.
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
Real | epsilon | 1e-9 | Relative accuracy tolerance of matrix symmetry |
Inductance | L[m,m] | Mutual inductance matrix |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | Positive quasi-static polyphase plug |
NegativePlug | plug_n | Negative quasi-static polyphase plug |
The impedance model represents a series connection of a resistor and either an inductor or capacitor
in each phase.

The linear impedance connects the voltage v with the
current i by v = Z*i in each phase, using m
singlephase impedances.
The resistive
components are modeled temperature dependent, so the real parts R_actual = real(Z) are determined from
the actual operating temperatures and the reference input resistances real(Z_ref).
Conditional heat ports are considered.
The reactive components X_actual = imag(Z)
are equal to imag(Z_ref) if frequencyDependent = false.
Frequency dependency is considered by frequencyDependent = true, distinguishing two cases:
imag(Z_ref) > 0: inductive caseX_actual are proportional to f/f_refimag(Z_ref) < 0: capacitive caseX_actual are proportional to f_ref/fImpedance, Resistor, Conductor, Capacitor, Inductor, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.MultiPhase.Interfaces.TwoPlug (Two plugs with pin-adapter) and Modelica.Electrical.MultiPhase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
ComplexImpedance | Z_ref[m] | Complex impedances R_ref + j*X_ref | |
Temperature | T_ref[m] | fill(293.15, m) | Reference temperatures |
LinearTemperatureCoefficient | alpha_ref[m] | zeros(m) | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) |
final Integer | mh | m | Number of heatPorts=number of phases |
Boolean | useHeatPort | false | =true, if all heat ports are enabled |
Temperature | T[mh] | T_ref | Fixed device temperatures if useHeatPort = false |
Boolean | frequencyDependent | false | Consider frequency dependency, if true |
Frequency | f_ref | 1 | Reference frequency, if frequency dependency is considered |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | Positive quasi-static polyphase plug |
NegativePlug | plug_n | Negative quasi-static polyphase plug |
HeatPort_a | heatPort[mh] | Conditional heat ports |
The admittance model represents a parallel connection of a resistor and either a capacitor or inductor
in each phase.
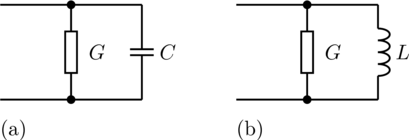
The linear admittance connects the voltage v with the
current i by i = Y*v in each phase, using m
singlephase admittances.
The resistive
components are modeled temperature dependent, so the real parts G_actual = real(Y) are determined from
the actual operating temperatures and the reference input conductances real(Y_ref).
Conditional heat ports are considered.
The reactive components
B_actual = imag(Y)
are equal to imag(Y_ref) if frequencyDependent = false.
Frequency dependency is considered by frequencyDependent = true, distinguishing two cases:
imag(Y_ref) > 0: capacitive caseB_actual are proportional to f/f_refimag(Y_ref) < 0: inductive caseB_actual are proportional to f_ref/fAdmittance, Resistor, Conductor, Capacitor, Impedance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.MultiPhase.Interfaces.TwoPlug (Two plugs with pin-adapter) and Modelica.Electrical.MultiPhase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
ComplexAdmittance | Y_ref[m] | Complex admittances G_ref + j*B_ref | |
Temperature | T_ref[m] | fill(293.15, m) | Reference temperatures |
LinearTemperatureCoefficient | alpha_ref[m] | zeros(m) | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) |
final Integer | mh | m | Number of heatPorts=number of phases |
Boolean | useHeatPort | false | =true, if all heat ports are enabled |
Temperature | T[mh] | T_ref | Fixed device temperatures if useHeatPort = false |
Boolean | frequencyDependent | false | Consider frequency dependency, if true |
Frequency | f_ref | 1 | Reference frequency, if frequency dependency is considered |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | Positive quasi-static polyphase plug |
NegativePlug | plug_n | Negative quasi-static polyphase plug |
HeatPort_a | heatPort[mh] | Conditional heat ports |
The linear resistors connect the complex voltages v with the complex
currents i by i*R = v,
using m single phase variable Resistors.
The resistances R are given as m input signals.
The resistor model also has m optional
conditional heat ports.
A linear temperature dependency of the resistances is also taken into account.
VariableResistor, Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.MultiPhase.Interfaces.TwoPlug (Two plugs with pin-adapter) and Modelica.Electrical.MultiPhase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
Temperature | T_ref[m] | fill(293.15, m) | Reference temperatures |
LinearTemperatureCoefficient | alpha_ref[m] | zeros(m) | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) |
final Integer | mh | m | Number of heatPorts=number of phases |
Boolean | useHeatPort | false | =true, if all heat ports are enabled |
Temperature | T[mh] | T_ref | Fixed device temperatures if useHeatPort = false |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | Positive quasi-static polyphase plug |
NegativePlug | plug_n | Negative quasi-static polyphase plug |
HeatPort_a | heatPort[mh] | Conditional heat ports |
input RealInput | R_ref[m] | Variable resistance |
The linear resistors connect the complex currents i with the complex
voltages v by v*G = i,
using m single phase variable Conductors.
The conductances G are given as m input signals.
The conductor model also has m optional
conditional heat ports.
A linear temperature dependency of the conductances is also taken into account.
VariableConductor, Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable capacitor, Variable inductor Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.MultiPhase.Interfaces.TwoPlug (Two plugs with pin-adapter) and Modelica.Electrical.MultiPhase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
Temperature | T_ref[m] | fill(293.15, m) | Reference temperatures |
LinearTemperatureCoefficient | alpha_ref[m] | zeros(m) | Temperature coefficient of resistance (G_actual = G_ref/(1 + alpha_ref*(heatPort.T - T_ref)) |
final Integer | mh | m | Number of heatPorts=number of phases |
Boolean | useHeatPort | false | =true, if all heat ports are enabled |
Temperature | T[mh] | T_ref | Fixed device temperatures if useHeatPort = false |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | Positive quasi-static polyphase plug |
NegativePlug | plug_n | Negative quasi-static polyphase plug |
HeatPort_a | heatPort[mh] | Conditional heat ports |
input RealInput | G_ref[m] | Variable conductance |
The linear capacitors connect the complex currents i with the complex
voltages v by v*j*ω*C = i,
using m single phase variable Capacitors.
The capacitances C are given as m input signals.
VariableCapacitor, Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable inductor Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.MultiPhase.Interfaces.TwoPlug (Two plugs with pin-adapter).
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | Positive quasi-static polyphase plug |
NegativePlug | plug_n | Negative quasi-static polyphase plug |
input RealInput | C[m] | Variable capacitance |
The linear inductors connect the complex voltages v with the complex
currents i by i*j*ω*L = v,
using m single phase variable Inductors.
The inductances L are given as m input signals.
Inductor, Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor Variable impedance, Variable admittance
Extends from Modelica.Electrical.QuasiStationary.MultiPhase.Interfaces.TwoPlug (Two plugs with pin-adapter).
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | Positive quasi-static polyphase plug |
NegativePlug | plug_n | Negative quasi-static polyphase plug |
input RealInput | L[m] | Variable inductance |
The impedance model represents a series connection of a resistor and either an inductor or capacitor
in each phase.

The linear impedance connects the complex voltage v with the
complex current i by i*Z = v in each phase,
using m
variable singlephase impedances.
The impedances Z_ref = R_ref + j*X_ref are given as complex input signals, representing the
resistive and reactive components of the input impedances. The resistive
components are modeled temperature dependent, so the real part R_actual = real(Z) are determined from
the actual operating temperatures and the reference input resistances real(Z_ref).
Conditional heat ports are considered.
The reactive components X_actual = imag(Z)
are equal to imag(Z_ref) if frequencyDependent = false.
Frequency dependency is considered by frequencyDependent = true, distinguishing two cases:
imag(Z_ref) > 0: inductive caseX_actual are proportional to f/f_refimag(Z_ref) < 0: capacitive caseX_actual are proportional to f_ref/f
Zero crossings of the real or imaginary parts of the impedance signals Z_ref could cause
singularities due to the actual structure of the connected network.
VariableResistor, Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable conductor, Variable capacitor, Variable inductor Variable admittance
Extends from Modelica.Electrical.QuasiStationary.MultiPhase.Interfaces.TwoPlug (Two plugs with pin-adapter) and Modelica.Electrical.MultiPhase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
Temperature | T_ref[m] | fill(293.15, m) | Reference temperatures |
LinearTemperatureCoefficient | alpha_ref[m] | zeros(m) | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) |
final Integer | mh | m | Number of heatPorts=number of phases |
Boolean | useHeatPort | false | =true, if all heat ports are enabled |
Temperature | T[mh] | T_ref | Fixed device temperatures if useHeatPort = false |
Boolean | frequencyDependent | false | Consider frequency dependency, if true |
Frequency | f_ref | 1 | Reference frequency, if frequency dependency is considered |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | Positive quasi-static polyphase plug |
NegativePlug | plug_n | Negative quasi-static polyphase plug |
HeatPort_a | heatPort[mh] | Conditional heat ports |
input ComplexInput | Z_ref[m] | Variable complex impedances |
The admittance model represents a parallel connection of a resistor and either a capacitor or inductor
in each phase.

The linear admittance connects the complex voltage v with the
complex current i by v*Y = i in each phase,
using m
variable singlephase admittances.
The admittances Y_ref = G_ref + j*B_ref are given as complex input signals, representing the
resistive and reactive components of the input admittances. The resistive
components are modeled temperature dependent, so the real part G_actual = real(Y) are determined from
the actual operating temperatures and the reference input conductances real(Y_ref).
Conditional heat ports are considered.
The reactive components B_actual = imag(Y)
are equal to imag(Y_ref) if frequencyDependent = false.
Frequency dependency is considered by frequencyDependent = true, distinguishing two cases:
imag(Y_ref) > 0: capacitive caseB_actual are proportional to f/f_refimag(Y_ref) < 0: inductive caseB_actual are proportional to f_ref/f
Zero crossings of the real or imaginary parts of the admittance signals Y_ref could cause
singularities due to the actual structure of the connected network.
VariableResistor, Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable conductor, Variable capacitor, Variable inductor Variable impedance,
Extends from Modelica.Electrical.QuasiStationary.MultiPhase.Interfaces.TwoPlug (Two plugs with pin-adapter) and Modelica.Electrical.MultiPhase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).
| Type | Name | Default | Description |
|---|---|---|---|
Integer | m | 3 | Number of phases |
Temperature | T_ref[m] | fill(293.15, m) | Reference temperatures |
LinearTemperatureCoefficient | alpha_ref[m] | zeros(m) | Temperature coefficient of resistance (R_actual = R_ref*(1 + alpha_ref*(heatPort.T - T_ref)) |
final Integer | mh | m | Number of heatPorts=number of phases |
Boolean | useHeatPort | false | =true, if all heat ports are enabled |
Temperature | T[mh] | T_ref | Fixed device temperatures if useHeatPort = false |
Boolean | frequencyDependent | false | Consider frequency dependency, if true |
Frequency | f_ref | 1 | Reference frequency, if frequency dependency is considered |
| Type | Name | Description |
|---|---|---|
PositivePlug | plug_p | Positive quasi-static polyphase plug |
NegativePlug | plug_n | Negative quasi-static polyphase plug |
HeatPort_a | heatPort[mh] | Conditional heat ports |
input ComplexInput | Y_ref[m] | Variable complex admittances |
Generated 2018-12-12 12:10:33 EST by MapleSim.