Package Modelica.​Math.​Distributions.​TruncatedWeibull
Library of truncated Weibull distribution functions

Information

This package provides

• probability density function (= derivative of cumulative distribution function),
• cumulative distribution function, and
• quantile (= inverse cumulative distribution function).

of the truncated Weibull distribution. Examples:

For more details
of the Weibull distribution, see Wikipedia,
of truncated distributions, see Wikipedia.

Extends from Modelica.​Icons.​Package (Icon for standard packages).

Package Contents

Function Modelica.​Math.​Distributions.​TruncatedWeibull.​density
Density of truncated Weibull distribution

Information

Syntax

Weibull.density(u, u_min=0, u_max=1, lambda=1, k=1);

Description

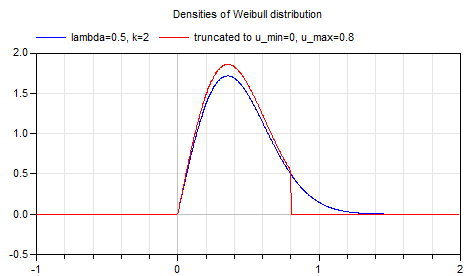
This function computes the probability density function according to a truncated Weibull distribution with minimum value u_min, maximum value u_max, scale parameter of original distribution lambda and shape parameter of original distribution k. Plot of the function:

For more details
of the Weibull distribution, see Wikipedia,
of truncated distributions, see Wikipedia.

Example

  density(0.5)             // = 0.9595173756674719
  density(0.5,0,0.8,0.5,2) // = 1.5948036466479143

See also

TruncatedWeibull.cumulative, TruncatedWeibull.quantile.

Extends from Modelica.​Math.​Distributions.​Interfaces.​partialTruncatedDensity (Common interface of truncated probability density functions).

Inputs

Outputs

Function Modelica.​Math.​Distributions.​TruncatedWeibull.​cumulative
Cumulative distribution function of truncated Weibull distribution

Information

Syntax

Weibull.cumulative(u, u_min=0, u_max=1, lambda=1, k=1);

Description

This function computes the cumulative distribution function according to a truncated Weibull distribution with minimum value u_min, maximum value u_max, scale parameter of original distribution lambda and shape parameter of original distribution k. The returned value y is in the range:

0 ≤ y ≤ 1

Plot of the function:

For more details
of the Weibull distribution, see Wikipedia,
of truncated distributions, see Wikipedia.

Example

  cumulative(0.5)             // = 0.6224593312018546
  cumulative(0.5,0,0.8,0.5,2) // = 0.6850805314988328

See also

TruncatedWeibull.density, TruncatedWeibull.quantile.

Extends from Modelica.​Math.​Distributions.​Interfaces.​partialTruncatedCumulative (Common interface of truncated cumulative distribution functions).

Inputs

Outputs

Function Modelica.​Math.​Distributions.​TruncatedWeibull.​quantile
Quantile of truncated Weibull distribution

Information

Syntax

Weibull.quantile(u, y_min=0, y_max=1, lambda=1, k=1);

Description

This function computes the inverse cumulative distribution function (= quantile) according to a truncated Weibull distribution with minimum value u_min, maximum value u_max, scale parameter of original distribution lambda and shape parameter of original distribution k. Input argument u must be in the range:

0 ≤ u ≤ 1

Output argument y is in the range:

y_min ≤ y ≤ y_max

Plot of the function:

For more details
of the Weibull distribution, see Wikipedia,
of truncated distributions, see Wikipedia.

Example

  quantile(0.001)           // = 0.0006323204312624211;
  quantile(0.5,0,1,0.5,0.9) // = 0.256951787882498

See also

TruncatedWeibull.density, TruncatedWeibull.cumulative.

Extends from Modelica.​Math.​Distributions.​Interfaces.​partialTruncatedQuantile (Common interface of truncated quantile functions (= inverse cumulative distribution functions)).

Inputs

Outputs

Generated 2018-12-12 12:14:35 EST by MapleSim.