Modelica.Clocked.RealSignals.Sampler.Utilities.Internal

Internal blocks and functions that are usually of no interest for the user

Information

The blocks in this package are internal that should usually not be utilized directly by the user (they are used as building blocks in "higher level" blocks).

Extends from Modelica.Icons.InternalPackage (Icon for an internal package (indicating that the package should not be directly utilized by user)).

Package Content

Name	Description
ComputationalDelay	Delay a clocked signal for at most one period, in order to model a computational delay
UniformNoise	Add band-limited uniform noise using a variant of the Wichmann-Hill algorithm
UniformNoiseXorshift64star	Add band-limited uniform noise based on a xorshift64* number generator
Quantization	DAC quantization effects
Limiter	Limit the range of a signal
random	Pseudo random number generator

Modelica.Clocked.RealSignals.Sampler.Utilities.Internal.ComputationalDelay

Delay a clocked signal for at most one period, in order to model a computational delay

Information

This block delays a clocked Real input signal by the fraction shiftCounter/resolution of the last interval. There is the restriction that shiftCounter/resolution ≤ 1.

Extends from Clocked.RealSignals.Interfaces.PartialClockedSISO (Block with clocked single input and clocked single output Real signals).

Parameters

Name	Description
Computational delay in seconds = interval() * shiftCounter/resolution
shiftCounter	(min=0, max=resolution), computational delay = interval()*shiftCounter/resolution
resolution	Time quantization resolution of sample interval

Connectors

Name	Description
u	Connector of clocked, Real input signal
y	Connector of clocked, Real output signal

Modelica.Clocked.RealSignals.Sampler.Utilities.Internal.UniformNoise

Add band-limited uniform noise using a variant of the Wichmann-Hill algorithm

Information

This block adds uniformly distributed noise in the range noiseMin … noiseMax to the clocked Real input signal and provides the sum as clocked Real output signal.

The Integer[3] parameter vector firstSeed is used to initialize the basic random number generator. The 3 elements of firstSeed need to be in the range [0, 255]. The use of the same seed vector will lead to the same sequence of numbers when these are computed serially. This is usually not desired. Therefore, for every usage of block Noise a different firstSeed should be defined.

This noise generator is based on a function that generates a random real number uniformly in the semi-open range [0.0, 1.0). The function uses the standard Wichmann-Hill generator, combining three pure multiplicative congruential generators of modulus 30269, 30307 and 30323. Its period (how many numbers it generates before repeating the sequence exactly) is 6,953,607,871,644. While of much higher quality than the rand() function supplied by most C libraries, the theoretical properties are much the same as for a single linear congruential generator of large modulus. For more details, see the underlying function Internal.random.

Example

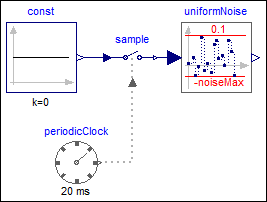
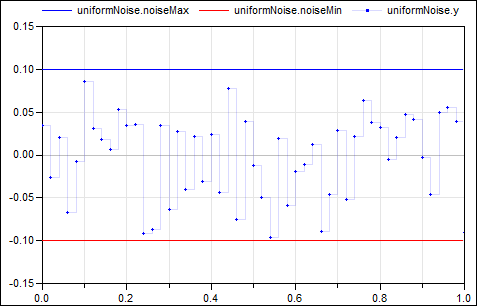
The following example samples zero signal with a periodic clock of 20 ms period, and adds noise in the range from -0.1 … 0.1:


	model	simulation result

Extends from Clocked.RealSignals.Interfaces.PartialNoise (Interface for SISO blocks with Real signals that add noise to the signal).

Parameters

Name	Description
noiseMax	Upper limit of noise band
noiseMin	Lower limit of noise band
firstSeed[3]	Integer[3] defining random sequence; required element range: 0..255

Connectors

Name	Description
u	Connector of clocked, Real input signal
y	Connector of clocked, Real output signal

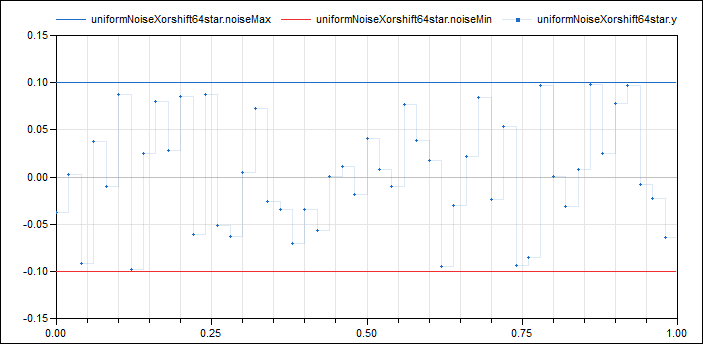
Modelica.Clocked.RealSignals.Sampler.Utilities.Internal.UniformNoiseXorshift64star

Add band-limited uniform noise based on a xorshift64* number generator

Information

This block adds uniformly distributed noise in the range noiseMin … noiseMax to the clocked Real input signal and provides the sum as clocked Real output signal.

It is based on the xorshift64* algorithm. For more details, see the documentation to Xorshift64star.

Example

The following example samples zero signal with a periodic clock of 20 ms period, and adds noise in the range from -0.1 … 0.1:


	model	simulation result

Extends from Clocked.RealSignals.Interfaces.PartialNoise (Interface for SISO blocks with Real signals that add noise to the signal).

Parameters

Name	Description
noiseMax	Upper limit of noise band
noiseMin	Lower limit of noise band
globalSeed	Global seed to initialize random number generator
localSeed	Local seed to initialize random number generator

Connectors

Name	Description
u	Connector of clocked, Real input signal
y	Connector of clocked, Real output signal

Modelica.Clocked.RealSignals.Sampler.Utilities.Internal.Quantization

DAC quantization effects

Information

The clocked Real input signal is value discretized (the discretization is defined by parameter bits).

Extends from Clocked.RealSignals.Interfaces.PartialClockedSISO (Block with clocked single input and clocked single output Real signals).

Parameters

Name	Description
quantized	= true, if quantization effects shall be computed
yMax	Upper limit of output
yMin	Lower limit of output
bits	Number of bits of quantization (if quantized = true)

Connectors

Name	Description
u	Connector of clocked, Real input signal
y	Connector of clocked, Real output signal

Modelica.Clocked.RealSignals.Sampler.Utilities.Internal.Limiter

Limit the range of a signal

Information

The Limiter block passes its input signal as output signal as long as the input is within the specified upper and lower limits. If this is not the case, the corresponding limits are passed as output.

Extends from Clocked.RealSignals.Interfaces.PartialClockedSISO (Block with clocked single input and clocked single output Real signals).

Parameters

Name	Description
uMax	Upper limits of input signals
uMin	Lower limits of input signals

Connectors

Name	Description
u	Connector of clocked, Real input signal
y	Connector of clocked, Real output signal

Modelica.Clocked.RealSignals.Sampler.Utilities.Internal.random

Pseudo random number generator

Information

Random generates a sequence of uniform distributed pseudo-random numbers. The algorithm is a variant of the multiplicative congruential algorithm, known as the Wichmann-Hill generator:

x(k) = (a1*x(k-1)) mod m1
y(k) = (a2*y(k-1)) mod m2
z(k) = (a3*z(k-1)) mod m3
U(k) = (x(k)/m1 + y(k)/m2 + z(k)/m3) mod 1

This generates pseudo-random numbers U(k) uniformly distributed in the interval (0,1). There are many forms of generators depending on the parameters m (prime numbers) and a. The sequence needs an initial Integer vector {x,y,z} known as the seed. The use of the same seed will lead to the same sequence of numbers.

Remarks

Random number generators (RNG) are pseudo-functions which are not true functions but algorithms which deliver a fixed sequence of (usually Integer) numbers which should have a very large period before they repeat itself and appropriate statistic properties such that the sequence appears to be a random draw. For real-valued random numbers, the integers are scaled to the real interval 0.0-1.0. They result in a uniformly distributed random variate between 0-1, which has to be transformed to give a random variate of a wanted distribution. There are two types of techniques for transforming random variates:

Acceptance-Rejection techniques
Transformation techniques

Acceptance-Rejection techniques throw away some of the generated variates and are thus less efficient. They can not be avoided for all distributions. A good summary about random number generation and most of the transformation techniques used below is given in:

Discrete Event Simulation
Jerry Banks and John S. Carson II
Prentice Hall Inc.
Englewood Cliffs, New Jersey

Some of the other references are quoted below.

WICHMANN-HILL RANDOM NUMBER GENERATOR
Wichmann, B. A. & Hill, I. D. (1982)
  Algorithm AS 183:
  An efficient and portable pseudo-random number generator
  Applied Statistics 31 (1982) 188-190
see also:
  Correction to Algorithm AS 183
  Applied Statistics 33 (1984) 123
McLeod, A. I. (1985)
  A remark on Algorithm AS 183
  Applied Statistics 34 (1985),198-200
In order to completely avoid external functions, all seeds are
set via parameters. For simulation purposes this is almost
always the desired behaviour.
Translated by Hubertus Tummescheit from Python source provided by
Guido van Rossum translated from C source by Adrian Baddeley.
http://www.python.org/doc/current/lib/module-random.html
R A N D O M   V A R I A B L E   G E N E R A T O R S
distributions on the real line:
------------------------------
    normal (Gaussian) 2 versions

Reference Literature

function random: Wichmann, B. A. & Hill, I. D. (1982), Algorithm AS 183:
An efficient and portable pseudo-random number generator, Applied Statistics 31 (1982) 188-190
see also: Correction to Algorithm AS 183, Applied Statistics 33 (1984) 123
McLeod, A. I. (1985), A remark on Algorithm AS 183, Applied Statistics 34 (1985),198-200
function normalvariate: Kinderman, A.J. and Monahan, J.F., 'Computer generation of random variables using the ratio of uniform deviates', ACM Trans Math Software, 3, (1977), pp257-260.
function gaussianvariate: Discrete Event Simulation, Jerry Banks and John S. Carson II,
Prentice Hall Inc. Englewood Cliffs, New Jersey, page 315/316

This Modelica function is free software; it can be redistributed and/or modified under the terms of the BSD-3-Clause license.

Extends from Modelica.Icons.Function (Icon for functions).

Inputs

Name	Description
seedIn[3]	Integer vector defining random number sequence, e.g., {23,87,187}

Outputs

Name	Description
x	Random number between 0 and 1
seedOut[3]	Modified seed to be used for next call of random()

Automatically generated Thu Oct 1 16:07:36 2020.