Modelica.Math.Vectors

Library of functions operating on vectors

Information

Library content

This library provides functions operating on vectors:

toString(v) - returns the string representation of vector v.
isEqual(v1, v2) - returns true if vectors v1 and v2 have the same size and the same elements.
norm(v,p) - returns the p-norm of vector v.
length(v) - returns the length of vector v (= norm(v,2), but inlined and therefore usable in symbolic manipulations)
normalize(v) - returns vector in direction of v with length = 1 and prevents zero-division for zero vector.
reverse(v) - reverses the vector elements of v.
sort(v) - sorts the elements of vector v in ascending or descending order.
find(e, v) - returns the index of the first occurrence of scalar e in vector v.
interpolate(x, y, xi) - returns the interpolated value in (x,y) that corresponds to xi.
relNodePositions(nNodes) - returns a vector of relative node positions (0..1).

Package Content

Name	Description
$Modelica.Math.Vectors.toString$ toString	Convert a real vector in to a string representation
$Modelica.Math.Vectors.isEqual$ isEqual	Determine if two Real vectors are numerically identical
$Modelica.Math.Vectors.norm$ norm	Return the p-norm of a vector
$Modelica.Math.Vectors.length$ length	Return length of a vector (better as norm(), if further symbolic processing is performed)
$Modelica.Math.Vectors.normalize$ normalize	Return normalized vector such that length = 1 and prevent zero-division for zero vector
$Modelica.Math.Vectors.normalizeWithAssert$ normalizeWithAssert	Return normalized vector such that length = 1 (trigger an assert for zero vector)
$Modelica.Math.Vectors.reverse$ reverse	Reverse vector elements (e.g., v[1] becomes last element)
$Modelica.Math.Vectors.sort$ sort	Sort elements of vector in ascending or descending order
$Modelica.Math.Vectors.find$ find	Find element in a vector
$Modelica.Math.Vectors.interpolate$ interpolate	Interpolate linearly in a vector
$Modelica.Math.Vectors.relNodePositions$ relNodePositions	Return vector of relative node positions (0..1)

$Modelica.Math.Vectors.toString$ Modelica.Math.Vectors.toString

Convert a real vector in to a string representation

Information

Syntax

Vectors.toString(v);
Vectors.toString(v,name="",significantDigits=6);

Description

The function call "Vectors.toString(v)" returns the string representation of vector v. With the optional arguments "name" and "significantDigits" a name and the number of the digits are defined. The default values of "name" and "significantDigits" are "" and 6 respectively. If name=="" (empty string) then the prefix "<name> =" is left out at the output-string.

Example

v = {2.12, -4.34, -2.56, -1.67};
toString(v);
                       // = "
                       //           2.12
                       //          -4.34
                       //          -2.56
                       //          -1.67"
toString(v,"vv",1);
                       // = "vv =
                       //           2
                       //          -4
                       //          -3
                       //          -2"

Inputs

Name	Description
v[:]	Real vector
name	Independent variable name used for printing
significantDigits	Number of significant digits that are shown

Outputs

Name	Description
s

$Modelica.Math.Vectors.isEqual$ Modelica.Math.Vectors.isEqual

Determine if two Real vectors are numerically identical

Information

Syntax

Vectors.isEqual(v1, v2);
Vectors.isEqual(v1, v2, eps=0);

Description

The function call "Vectors.isEqual(v1, v2)" returns true, if the two Real vectors v1 and v2 have the same dimensions and the same elements. Otherwise the function returns false. Two elements e1 and e2 of the two vectors are checked on equality by the test "abs(e1-e2) ≤ eps", where "eps" can be provided as third argument of the function. Default is "eps = 0".

Example

  Real v1[3] = {1, 2, 3};
  Real v2[4] = {1, 2, 3, 4};
  Real v3[3] = {1, 2, 3.0001};
  Boolean result;
algorithm
  result := Vectors.isEqual(v1,v2);     // = false
  result := Vectors.isEqual(v1,v3);     // = false
  result := Vectors.isEqual(v1,v1);     // = true
  result := Vectors.isEqual(v1,v3,0.1); // = true

Inputs

Name	Description
v1[:]	First vector
v2[:]	Second vector (may have different length as v1)
eps	Two elements e1 and e2 of the two vectors are identical if abs(e1-e2) <= eps

Outputs

Name	Description
result	= true, if vectors have the same length and the same elements

$Modelica.Math.Vectors.norm$ Modelica.Math.Vectors.norm

Return the p-norm of a vector

Information

Syntax

Vectors.norm(v);
Vectors.norm(v,p=2);   // 1 ≤ p ≤ ∞

Description

The function call "Vectors.norm(v)" returns the Euclidean norm "sqrt(v*v)" of vector v. With the optional second argument "p", any other p-norm can be computed:

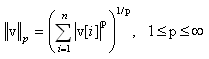
$function Vectors.norm$

Besides the Euclidean norm (p=2), also the 1-norm and the infinity-norm are sometimes used:

1-norm	= sum(abs(v))	norm(v,1)
2-norm	= sqrt(v*v)	norm(v) or norm(v,2)
infinity-norm	= max(abs(v))	norm(v,Modelica.Constants.inf)

Note, for any vector norm the following inequality holds:

norm(v1+v2,p) ≤ norm(v1,p) + norm(v2,p)

Example

v = {2, -4, -2, -1};
norm(v,1);    // = 9
norm(v,2);    // = 5
norm(v);      // = 5
norm(v,10.5); // = 4.00052597412635
norm(v,Modelica.Constants.inf);  // = 4

Inputs

Name	Description
v[:]	Real vector
p	Type of p-norm (often used: 1, 2, or Modelica.Constants.inf)

Outputs

Name	Description
result	p-norm of vector v

$Modelica.Math.Vectors.length$ Modelica.Math.Vectors.length

Return length of a vector (better as norm(), if further symbolic processing is performed)

Information

Syntax

Vectors.length(v);

Description

The function call "Vectors.length(v)" returns the Euclidean length "sqrt(v*v)" of vector v. The function call is equivalent to Vectors.norm(v). The advantage of length(v) over norm(v) is that function length(..) is implemented in one statement and therefore the function is usually automatically inlined. Further symbolic processing is therefore possible, which is not the case with function norm(..).

Example

v = {2, -4, -2, -1};
length(v);  // = 5

Inputs

Name	Description
v[:]	Real vector

Outputs

Name	Description
result	Length of vector v

$Modelica.Math.Vectors.normalize$ Modelica.Math.Vectors.normalize

Return normalized vector such that length = 1 and prevent zero-division for zero vector

Information

Syntax

Vectors.normalize(v);
Vectors.normalize(v,eps=100*Modelica.Constants.eps);

Description

The function call "Vectors.normalize(v)" returns the unit vector "v/length(v)" of vector v. If length(v) is close to zero (more precisely, if length(v) < eps), v/eps is returned in order to avoid a division by zero. For many applications this is useful, because often the unit vector e = v/length(v) is used to compute a vector x*e, where the scalar x is in the order of length(v), i.e., x*e is small, when length(v) is small and then it is fine to replace e by v to avoid a division by zero.

Since the function has the "Inline" annotation, it is usually inlined and symbolic processing is applied.

Example

normalize({1,2,3});  // = {0.267, 0.534, 0.802}
normalize({0,0,0});  // = {0,0,0}

Inputs

Name	Description
v[:]	Real vector
eps	if \|v\| < eps then result = v/eps

Outputs

Name	Description
result[size(v, 1)]	Input vector v normalized to length=1

$Modelica.Math.Vectors.normalizeWithAssert$ Modelica.Math.Vectors.normalizeWithAssert

Return normalized vector such that length = 1 (trigger an assert for zero vector)

Information

Syntax

Vectors.normalizeWithAssert(v);

Description

The function call "Vectors.normalizeWithAssert(v)" returns the unit vector "v/sqrt(v*v)" of vector v. If vector v is a zero vector, an assert is triggered.

Since the function has the "Inline" annotation, it is usually inlined and symbolic processing is applied.

Example

normalizeWithAssert({1,2,3});  // = {0.267, 0.534, 0.802}
normalizeWithAssert({0,0,0});  // error (an assert is triggered)

Inputs

Name	Description
v[:]	Real vector

Outputs

Name	Description
result[size(v, 1)]	Input vector v normalized to length=1

$Modelica.Math.Vectors.reverse$ Modelica.Math.Vectors.reverse

Reverse vector elements (e.g., v[1] becomes last element)

Information

Syntax

Vectors.reverse(v);

Description

The function call "Vectors.reverse(v)" returns the vector elements in reverse order.

Example

reverse({1,2,3,4});  // = {4,3,2,1}

Extends from Modelica.Icons.Function (Icon for functions).

Inputs

Name	Description
v[:]	Real vector

Outputs

Name	Description
result[size(v, 1)]	Elements of vector v in reversed order

$Modelica.Math.Vectors.sort$ Modelica.Math.Vectors.sort

Sort elements of vector in ascending or descending order

Information

Syntax

           sorted_v = Vectors.sort(v);
(sorted_v, indices) = Vectors.sort(v, ascending=true);

Description

Function sort(..) sorts a Real vector v in ascending order and returns the result in sorted_v. If the optional argument "ascending" is false, the vector is sorted in descending order. In the optional second output argument the indices of the sorted vector with respect to the original vector are given, such that sorted_v = v[indices].

Example

(v2, i2) := Vectors.sort({-1, 8, 3, 6, 2});
     -> v2 = {-1, 2, 3, 6, 8}
        i2 = {1, 5, 3, 4, 2}

Extends from Modelica.Icons.Function (Icon for functions).

Inputs

Name	Description
v[:]	Real vector to be sorted
ascending	= true, if ascending order, otherwise descending order

Outputs

Name	Description
sorted_v[size(v, 1)]	Sorted vector
indices[size(v, 1)]	sorted_v = v[indices]

$Modelica.Math.Vectors.find$ Modelica.Math.Vectors.find

Find element in a vector

Information

Syntax

Vectors.find(e, v);
Vectors.find(e, v, eps=0);

Description

The function call "Vectors.find(e, v)" returns the index of the first occurrence of input e in vector v. The test of equality is performed by "abs(e-v[i]) ≤ eps", where "eps" can be provided as third argument of the function. Default is "eps = 0".

Example

  Real v[3] = {1, 2, 3};
  Real e1 = 2;
  Real e2 = 3.01;
  Boolean result;
algorithm
  result := Vectors.find(e1,v);          // = 2
  result := Vectors.find(e2,v);          // = 0
  result := Vectors.find(e2,v,eps=0.1);  // = 3

Inputs

Name	Description
e	Search for e
v[:]	Real vector
eps	Element e is equal to a element v[i] of vector v if abs(e-v[i]) <= eps

Outputs

Name	Description
result	v[result] = e (first occurrence of e); result=0, if not found

$Modelica.Math.Vectors.interpolate$ Modelica.Math.Vectors.interpolate

Interpolate linearly in a vector

Information

Syntax

// Real    x[:], y[:], xi, yi;
// Integer iLast, iNew;
        yi = Vectors.interpolate(x,y,xi);
(yi, iNew) = Vectors.interpolate(x,y,xi,iLast=1);

Description

The function call "Vectors.interpolate(x,y,xi)" interpolates linearly in vectors (x,y) and returns the value yi that corresponds to xi. Vector x[:] must consist of monotonically increasing values. If xi < x[1] or > x[end], then extrapolation takes places through the first or last two x[:] values, respectively. If the x and y vectors have length 1, then always y[1] is returned. The search for the interval x[iNew] ≤ xi < x[iNew+1] starts at the optional input argument "iLast". The index "iNew" is returned as output argument. The usage of "iLast" and "iNew" is useful to increase the efficiency of the call, if many interpolations take place. If x has two or more identical values then interpolation utilizes the x-value with the largest index.

Example

  Real x1[:] = { 0,  2,  4,  6,  8, 10};
  Real x2[:] = { 1,  2,  3,  3,  4,  5};
  Real y[:]  = {10, 20, 30, 40, 50, 60};
algorithm
  (yi, iNew) := Vectors.interpolate(x1,y,5);  // yi = 35, iNew=3
  (yi, iNew) := Vectors.interpolate(x2,y,4);  // yi = 50, iNew=5
  (yi, iNew) := Vectors.interpolate(x2,y,3);  // yi = 40, iNew=4

Extends from Modelica.Icons.Function (Icon for functions).

Inputs

Name	Description
x[:]	Abscissa table vector (strict monotonically increasing values required)
y[size(x, 1)]	Ordinate table vector
xi	Desired abscissa value
iLast	Index used in last search

Outputs

Name	Description
yi	Ordinate value corresponding to xi
iNew	xi is in the interval x[iNew] <= xi < x[iNew+1]

$Modelica.Math.Vectors.relNodePositions$ Modelica.Math.Vectors.relNodePositions

Return vector of relative node positions (0..1)

Information

Syntax

Vectors.relNodePositions(nNodes);

Description

The function call "relNodePositions(nNodes)" returns a vector with the relative positions of the nodes of a discretized pipe with nNodes nodes (including the node at the left and at the right side of the pipe), see next figure:

Example

  Real xsi[7];
algorithm
  xsi = relNodePositions(7);  // xsi = {0, 0.1, 0.3, 0.5, 0.7, 0.9, 1}

Inputs

Name	Description
nNodes	Number of nodes (including node at left and right position)

Outputs

Name	Description
xsi[nNodes]	Relative node positions

Automatically generated Thu Oct 1 16:08:15 2020.

Modelica.Math.Vectors

Information

Library content

See also

Package Content

Modelica.Math.Vectors.toString

Information

Syntax

Description

Example

See also

Inputs

Outputs

Modelica.Math.Vectors.isEqual

Information

Syntax

Description

Example

See also

Inputs

Outputs

Modelica.Math.Vectors.norm

Information

Syntax

Description

Example

See also

Inputs

Outputs

Modelica.Math.Vectors.length

Information

Syntax

Description

Example

See also

Inputs

Outputs

Modelica.Math.Vectors.normalize

Information

Syntax

Description

Example

See also

Inputs

Outputs

Modelica.Math.Vectors.normalizeWithAssert

Information

Syntax

Description

Example

See also

Inputs

Outputs

Modelica.Math.Vectors.reverse

Information

Syntax

Description

Example

Inputs

Outputs

Modelica.Math.Vectors.sort

Information

Syntax

Description

Example

Inputs

Outputs

Modelica.Math.Vectors.find

Information

Syntax

Description

Example

See also

Inputs

Outputs

Modelica.Math.Vectors.interpolate

Information

Syntax

Description

Example

$Modelica.Math.Vectors.toString$ Modelica.Math.Vectors.toString

$Modelica.Math.Vectors.isEqual$ Modelica.Math.Vectors.isEqual

$Modelica.Math.Vectors.norm$ Modelica.Math.Vectors.norm

$Modelica.Math.Vectors.length$ Modelica.Math.Vectors.length

$Modelica.Math.Vectors.normalize$ Modelica.Math.Vectors.normalize

$Modelica.Math.Vectors.normalizeWithAssert$ Modelica.Math.Vectors.normalizeWithAssert

$Modelica.Math.Vectors.reverse$ Modelica.Math.Vectors.reverse

$Modelica.Math.Vectors.sort$ Modelica.Math.Vectors.sort

$Modelica.Math.Vectors.find$ Modelica.Math.Vectors.find

$Modelica.Math.Vectors.interpolate$ Modelica.Math.Vectors.interpolate

$Modelica.Math.Vectors.relNodePositions$ Modelica.Math.Vectors.relNodePositions