Modelica.Mechanics.Translational.Components

Components for 1D translational mechanical drive trains

Information

This package contains basic components 1D mechanical translational drive trains.

Extends from Modelica.Icons.Package (Icon for standard packages).

Package Content

Name	Description
Fixed	Fixed flange
Mass	Sliding mass with inertia
Rod	Rod without inertia
Spring	Linear 1D translational spring
Damper	Linear 1D translational damper
SpringDamper	Linear 1D translational spring and damper in parallel
ElastoGap	1D translational spring damper combination with gap
SupportFriction	Coulomb friction in support
Brake	Brake based on Coulomb friction
IdealGearR2T	Gearbox transforming rotational into translational motion
IdealRollingWheel	Simple 1-dim. model of an ideal rolling wheel without inertia
RollingResistance	Resistance of a rolling wheel
Vehicle	Simple vehicle model
InitializeFlange	Initializes a flange with pre-defined position, speed and acceleration (usually, this is reference data from a control bus)
MassWithStopAndFriction	Sliding mass with hard stop and Stribeck friction
RelativeStates	Definition of relative state variables
GeneralForceToPositionAdaptor	Signal adaptor for a Translational flange with position, speed, and acceleration as outputs and force as input (especially useful for FMUs)
GeneralPositionToForceAdaptor	Signal adaptor for a Translational flange with force as output and position, speed and acceleration as input (especially useful for FMUs)

Modelica.Mechanics.Translational.Components.Fixed

Fixed flange

Information

The flange of a 1D translational mechanical system fixed at an position s0 in the housing. May be used:

• to connect a compliant element, such as a spring or a damper, between a sliding mass and the housing.
• to fix a rigid element, such as a sliding mass, at a specific position.

Parameters

Connectors

Modelica.Mechanics.Translational.Components.Mass

Sliding mass with inertia

Information

Sliding mass with inertia, without friction and two rigidly connected flanges.

The sliding mass has the length L, the position coordinate s is in the middle. Sign convention: A positive force at flange flange_a moves the sliding mass in the positive direction. A negative force at flange flange_a moves the sliding mass to the negative direction.

Extends from Translational.Interfaces.PartialRigid (Rigid connection of two translational 1D flanges).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.Rod

Rod without inertia

Information

A translational rod without inertia and two rigidly connected flanges.

Extends from Translational.Interfaces.PartialRigid (Rigid connection of two translational 1D flanges).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.Spring

Linear 1D translational spring

Information

A linear 1D translational spring. The component can be connected either between two sliding masses, or between a sliding mass and the housing (model Fixed), to describe a coupling of the sliding mass with the housing via a spring.

Extends from Translational.Interfaces.PartialCompliant (Compliant connection of two translational 1D flanges).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.Damper

Linear 1D translational damper

Information

Linear, velocity dependent damper element. It can be either connected between a sliding mass and the housing (model Fixed), or between two sliding masses.

Extends from Translational.Interfaces.PartialCompliantWithRelativeStates (Base model for the compliant connection of two translational 1-dim. shaft flanges where the relative position and relative velocities are used as states), Modelica.Thermal.HeatTransfer.Interfaces.PartialElementaryConditionalHeatPortWithoutT (Partial model to include a conditional HeatPort in order to dissipate losses, used for textual modeling, i.e., for elementary models).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.SpringDamper

Linear 1D translational spring and damper in parallel

Information

A spring and damper element connected in parallel. The component can be connected either between two sliding masses to describe the elasticity and damping, or between a sliding mass and the housing (model Fixed), to describe a coupling of the sliding mass with the housing via a spring/damper.

Extends from Translational.Interfaces.PartialCompliantWithRelativeStates (Base model for the compliant connection of two translational 1-dim. shaft flanges where the relative position and relative velocities are used as states), Modelica.Thermal.HeatTransfer.Interfaces.PartialElementaryConditionalHeatPortWithoutT (Partial model to include a conditional HeatPort in order to dissipate losses, used for textual modeling, i.e., for elementary models).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.ElastoGap

1D translational spring damper combination with gap

Information

This component models a spring damper combination that can lift off. It can be connected between a sliding mass and the housing (model Fixed), to describe the contact of a sliding mass with the housing.

As long as s_rel > s_rel0, no force is exerted (s_rel = flange_b.s - flange_a.s). If s_rel ≤ s_rel0, the contact force is basically computed with a linear spring/damper characteristic. With parameter n≥1 (exponent of spring force), a nonlinear spring force can be modeled:

desiredContactForce = c*|s_rel - s_rel0|^n + d*der(s_rel)

Note, Hertzian contact is described by:

• Contact between two metallic spheres: n=1.5
• Contact between two metallic plates: n=1

The above force law leads to the following difficulties:

1. If the damper force becomes larger as the spring force and with opposite sign, the contact force would be "pulling/sticking" which is unphysical, since during contact only pushing forces can occur.
2. When contact occurs with a non-zero relative speed (which is the usual situation), the damping force has a non-zero value and therefore the contact force changes discontinuously at s_rel = s_rel0. Again, this is not physical because the force can only change continuously. (Note, this component is not an idealized model where a steep characteristic is approximated by a discontinuity, but it shall model the steep characteristic.)

In the literature there are several proposals to fix problem (2). Especially, often the following model is used (see, e.g., Lankarani, Nikravesh: Continuous Contact Force Models for Impact Analysis in Multibody Systems, Nonlinear Dynamics 5, pp. 193-207, 1994, pdf-download):

f = c*s_rel^n + (d*s_rel^n)*der(s_rel)

However, this and other models proposed in literature violate issue (1), i.e., unphysical pulling forces can occur (if d*der(s_rel) becomes large enough). Note, if the force law is of the form "f = f_c + f_d", then a necessary condition is that |f_d| ≤ |f_c|, otherwise (1) and (2) are violated. For this reason, the most simplest approach is used in the ElastoGap model to fix both problems by using this necessary condition in the force law directly. If s_rel0 = 0, the equations are:

if s_rel ≥ 0 then
   f = 0;    // contact force
else
   f_c  = -c*|s_rel|^n;          // contact spring force (Hertzian contact force)
   f_d2 = d*der(s_rel);         // linear contact damper force
   f_d  = if f_d2 <  f_c then  f_c else
          if f_d2 > -f_c then -f_c else f_d2;  // bounded damper force
   f    = f_c + f_d;            // contact force
end if;

Note, since |f_d| ≤ |f_c|, pulling forces cannot occur and the contact force is always continuous, especially around the start of the penetration at s_rel = s_rel0.

In the next figure, a typical simulation with the ElastoGap model is shown (Examples.ElastoGap) where the different effects are visualized:

1. Curve 1 (elastoGap1.f) is the unmodified contact force, i.e., the linear spring/damper characteristic. A pulling/sticking force is present at the end of the contact.
2. Curve 2 (elastoGap2.f) is the contact force, where the force is explicitly set to zero when pulling/sticking occurs. The contact force is discontinuous when contact starts.
3. Curve 3 (elastoGap3.f) is the ElastoGap model of this library. No discontinuity and no pulling/sticking occurs.

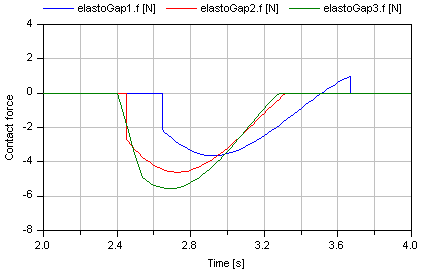
Extends from Modelica.Mechanics.Translational.Interfaces.PartialCompliantWithRelativeStates (Base model for the compliant connection of two translational 1-dim. shaft flanges where the relative position and relative velocities are used as states), Modelica.Thermal.HeatTransfer.Interfaces.PartialElementaryConditionalHeatPortWithoutT (Partial model to include a conditional HeatPort in order to dissipate losses, used for textual modeling, i.e., for elementary models).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.SupportFriction

Coulomb friction in support

Information

This element describes Coulomb friction in support, i.e., a frictional force acting between a flange and the housing. The positive sliding friction force "f" has to be defined by table "f_pos" as function of the absolute velocity "v". E.g.

 v |   f
---+-----
 0 |   0
 1 |   2
 2 |   5
 3 |   8

gives the following table:

f_pos = [0, 0; 1, 2; 2, 5; 3, 8];

Currently, only linear interpolation in the table is supported. Outside of the table, extrapolation through the last two table entries is used. It is assumed that the negative sliding friction force has the same characteristic with negative values. Friction is modelled in the following way:

When the absolute velocity "v" is not zero, the friction force is a function of v and of a constant normal force. This dependency is defined via table f_pos and can be determined by measurements, e.g., by driving the gear with constant velocity and measuring the needed driving force (= friction force).

When the absolute velocity becomes zero, the elements connected by the friction element become stuck, i.e., the absolute position remains constant. In this phase the friction force is calculated from a force balance due to the requirement, that the absolute acceleration shall be zero. The elements begin to slide when the friction force exceeds a threshold value, called the maximum static friction force, computed via:

maximum_static_friction = peak * sliding_friction(v=0)  (peak >= 1)

This procedure is implemented in a "clean" way by state events and leads to continuous/discrete systems of equations if friction elements are dynamically coupled which have to be solved by appropriate numerical methods. The method is described in (see also a short sketch in UsersGuide.ModelingOfFriction):

Otter M., Elmqvist H., and Mattsson S.E. (1999):

Hybrid Modeling in Modelica based on the Synchronous Data Flow Principle. CACSD'99, Aug. 22.-26, Hawaii.

More precise friction models take into account the elasticity of the material when the two elements are "stuck", as well as other effects, like hysteresis. This has the advantage that the friction element can be completely described by a differential equation without events. The drawback is that the system becomes stiff (about 10-20 times slower simulation) and that more material constants have to be supplied which requires more sophisticated identification. For more details, see the following references, especially (Armstrong and Canudas de Wit 1996):

Armstrong B. (1991):

Control of Machines with Friction. Kluwer Academic Press, Boston MA.

Armstrong B., and Canudas de Wit C. (1996):

Friction Modeling and Compensation. The Control Handbook, edited by W.S.Levine, CRC Press, pp. 1369-1382.

Canudas de Wit C., Olsson H., Åström K.J., and Lischinsky P. (1995):

A new model for control of systems with friction. IEEE Transactions on Automatic Control, Vol. 40, No. 3, pp. 419-425.

Extends from Modelica.Mechanics.Translational.Interfaces.PartialElementaryTwoFlangesAndSupport2 (Partial model for a component with one translational 1-dim. shaft flange and a support used for textual modeling, i.e., for elementary models), Modelica.Thermal.HeatTransfer.Interfaces.PartialElementaryConditionalHeatPortWithoutT (Partial model to include a conditional HeatPort in order to dissipate losses, used for textual modeling, i.e., for elementary models), Translational.Interfaces.PartialFriction (Base model of Coulomb friction elements).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.Brake

Brake based on Coulomb friction

Information

This component models a brake, i.e., a component where a frictional force is acting between the housing and a flange and a controlled normal force presses the flange to the housing in order to increase friction. The normal force fn has to be provided as input signal f_normalized in a normalized form (0 ≤ f_normalized ≤ 1), fn = fn_max*f_normalized, where fn_max has to be provided as parameter. Friction in the brake is modelled in the following way:

When the absolute velocity "v" is not zero, the friction force is a function of the velocity dependent friction coefficient mu(v), of the normal force "fn", and of a geometry constant "cgeo" which takes into account the geometry of the device and the assumptions on the friction distributions:

frictional_force = cgeo * mu(v) * fn

Typical values of coefficients of friction mu:

• 0.2 … 0.4 for dry operation,
• 0.05 … 0.1 when operating in oil.

The positive part of the friction characteristic mu(v), v >= 0, is defined via table mu_pos (first column = v, second column = mu). Currently, only linear interpolation in the table is supported.

When the absolute velocity becomes zero, the elements connected by the friction element become stuck, i.e., the absolute position remains constant. In this phase the friction force is calculated from a force balance due to the requirement, that the absolute acceleration shall be zero. The elements begin to slide when the friction force exceeds a threshold value, called the maximum static friction force, computed via:

frictional_force = peak * cgeo * mu(w=0) * fn   (peak >= 1)

This procedure is implemented in a "clean" way by state events and leads to continuous/discrete systems of equations if friction elements are dynamically coupled. The method is described in:

Otter M., Elmqvist H., and Mattsson S.E. (1999):

Hybrid Modeling in Modelica based on the Synchronous Data Flow Principle. CACSD'99, Aug. 22.-26, Hawaii.

More precise friction models take into account the elasticity of the material when the two elements are "stuck", as well as other effects, like hysteresis. This has the advantage that the friction element can be completely described by a differential equation without events. The drawback is that the system becomes stiff (about 10-20 times slower simulation) and that more material constants have to be supplied which requires more sophisticated identification. For more details, see the following references, especially (Armstrong and Canudas de Wit 1996):

Armstrong B. (1991):

Control of Machines with Friction. Kluwer Academic Press, Boston MA.

Armstrong B., and Canudas de Wit C. (1996):

Friction Modeling and Compensation. The Control Handbook, edited by W.S.Levine, CRC Press, pp. 1369-1382.

Canudas de Wit C., Olsson H., Åström K.J., and Lischinsky P. (1995):

A new model for control of systems with friction. IEEE Transactions on Automatic Control, Vol. 40, No. 3, pp. 419-425.

Extends from Modelica.Mechanics.Translational.Interfaces.PartialElementaryTwoFlangesAndSupport2 (Partial model for a component with one translational 1-dim. shaft flange and a support used for textual modeling, i.e., for elementary models), Modelica.Thermal.HeatTransfer.Interfaces.PartialElementaryConditionalHeatPortWithoutT (Partial model to include a conditional HeatPort in order to dissipate losses, used for textual modeling, i.e., for elementary models), Translational.Interfaces.PartialFriction (Base model of Coulomb friction elements).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.IdealGearR2T

Gearbox transforming rotational into translational motion

Information

Couples rotational and translational motion, like a toothed wheel with a toothed rack, specifying the ratio of rotational / translational motion.

Extends from Modelica.Mechanics.Rotational.Components.IdealGearR2T (Gearbox transforming rotational into translational motion).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.IdealRollingWheel

Simple 1-dim. model of an ideal rolling wheel without inertia

Information

Couples rotational and translational motion, like an ideal rolling wheel, specifying the wheel radius.

Extends from Modelica.Mechanics.Rotational.Components.IdealRollingWheel (Simple 1-dim. model of an ideal rolling wheel without inertia).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.RollingResistance

Resistance of a rolling wheel

Information

Simplified model of the resistance of a rolling wheel, dependent on vertical wheel load (due to gravity, i.e. static only), inclination and rolling resistance coefficient:

flange.f = Cr * fWeight * cos(alpha)

The rolling resistance coefficient C_r is either constant (given by the parameter CrConstant) or prescribed by the input cr.

The inclination is either constant (parameter inclinationConstant) or prescribed by the input inclination. This corresponds to the road rise over running distance of 100 m which, in general, is written as a percentage and is equal to tan(α). For example for a road rising by 10 m over 100 m the grade = 10 % and, thus, the inclination is 0.1. Positive inclination means driving uphill, negative inclination means driving downhill, in case of positive vehicle velocity.

Note

The rolling resistance is independent of velocity here, but changes its direction with the direction of velocity. To avoid numerical problems around zero velocity, the rolling resistance is regularized accordingly within [-v0, v0]. Therefore static friction at vehicle's standstill is not taken into account.

Extends from Modelica.Mechanics.Translational.Interfaces.PartialForce (Partial model of a force acting at the flange (accelerates the flange)).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.Vehicle

Simple vehicle model

Information

This is a simple model of a ground vehicle, comprising the mass, the aerodynamic drag, the rolling resistance and the inclination resistance (caused by the road grade). For all particular resistances, significant variables can be either given by a parameter or input by a time-variable signal.

The vehicle can be driven at the rotational flange flangeR, e.g. by an electric motor and a gearbox. It is possible to use the vehicle as a passive trailer, leaving the rotational flange flangeR unconnected.

At the translational flange flangeT the vehicle can be coupled with another vehicle, e.g. as a trailer or to pull a trailer. It is possible to leave the translational flange flangeT unconnected.

The velocity v and the driven distance s of the vehicle are provided as variables; the vehicle can be initialized using these variables.

Mass and inertia

Both the translational vehicle mass and the rotational inertias (e.g. the wheels) are accelerated when the vehicle is accelerated. This nature is usually put into account for fundamental vehicle analyses done either in the rotational or translational domain, e.g. when analysing vehicle's driveline. Then, the vehicle mass m can be expressed as an additional equivalent inertia J_eq = m * R2 or vice versa rotational inertia J as an additional equivalent mass m_eq = J/R2, where R is the wheel radius. Since this model introduces rolling resistance and inclination resistance as well where just the vehicle mass plays a role, the approach of equivalent mass/inertia would lead to incorrect simulation results and shall therefore not be applied here.

Drag resistance

fDrag = Cd*rho*A*(v - vWind)^2/2

Wind velocity is measured in the same direction as velocity of flangeT. Wind velocity is either constant or prescribed by the input vWind.

Rolling resistance

fRoll = Cr*m*g*cos(alpha)

Rolling resistance coefficient Cr is either constant or prescribed by the input cr. Rolling resistance has a crossover from positive to negative velocity within [-vReg, vReg].

The inclination angle α is either constant or prescribed by the input inclination = tan(α). This corresponds to the road rise over running distance of 100 m which, in general, is written as a percentage. For example for a road rising by 10 m over 100 m the grade = 10 % and, thus, the parameter inclinationConstant = 0.1. Positive inclination means driving uphill, negative inclination means driving downhill, in case of positive vehicle velocity.

Inclination resistance

fGrav = m*g*sin(alpha)

With the inclination angle α described above.

Parameters

Connectors

Modelica.Mechanics.Translational.Components.InitializeFlange

Initializes a flange with pre-defined position, speed and acceleration (usually, this is reference data from a control bus)

Information

This component is used to optionally initialize the position, speed, and/or acceleration of the flange to which this component is connected. Via parameters use_s_start, use_v_start, use_a_start the corresponding input signals s_start, v_start, a_start are conditionally activated. If an input is activated, the corresponding flange property is initialized with the input value at start time.

For example, if "use_s_start = true", then flange.s is initialized with the value of the input signal "s_start" at the start time.

Additionally, it is optionally possible to define the "StateSelect" attribute of the flange position and the flange speed via parameter "stateSelection".

This component is especially useful when the initial values of a flange shall be set according to reference signals of a controller that are provided via a signal bus.

Extends from Modelica.Blocks.Icons.Block (Basic graphical layout of input/output block).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.MassWithStopAndFriction

Sliding mass with hard stop and Stribeck friction

Information

This element describes the Stribeck friction characteristics of a sliding mass, i. e. the frictional force acting between the sliding mass and the support. Included is a hard stop for the position.

The surface is fixed and there is friction between sliding mass and surface. The frictional force f is given for positive velocity v by:

f = F_Coulomb + F_prop * v + F_Stribeck * exp (-fexp * v)

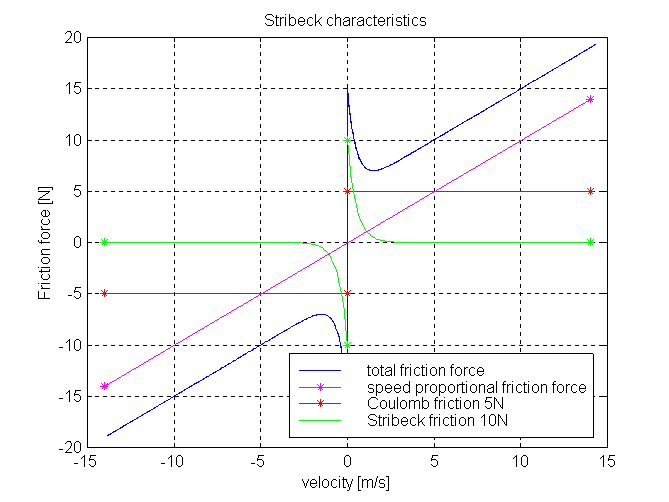
The distance between the left and the right connector is given by parameter L. The position of the center of gravity, coordinate s, is in the middle between the two flanges.

There are hard stops at smax and smin, i. e. if flange_a.s >= smin and flange_b.s <= xmax the sliding mass can move freely.

When the absolute velocity becomes zero, the sliding mass becomes stuck, i.e., the absolute position remains constant. In this phase the friction force is calculated from a force balance due to the requirement that the absolute acceleration shall be zero. The elements begin to slide when the friction force exceeds a threshold value, called the maximum static friction force, computed via:

maximum_static_friction =  F_Coulomb + F_Stribeck

This requires the states Stop.s and Stop.v . If these states are eliminated during the index reduction the model will not work. To avoid this any inertias should be connected via springs to the Stop element, other sliding masses, dampers or hydraulic chambers must be avoided.

For more details of the used friction model see the following reference:

Beater P. (1999):

Entwurf hydraulischer Maschinen (in German), Springer Verlag Berlin Heidelberg New York, DOI 10.1007/978-3-642-58395-7.

The friction model is implemented in a "clean" way by state events and leads to continuous/discrete systems of equations which have to be solved by appropriate numerical methods. The method is described in (see also a short sketch in UsersGuide.ModelingOfFriction):

Otter M., Elmqvist H., and Mattsson S.E. (1999):

Hybrid Modeling in Modelica based on the Synchronous Data Flow Principle. CACSD'99, Aug. 22.-26, Hawaii.

More precise friction models take into account the elasticity of the material when the two elements are "stuck", as well as other effects, like hysteresis. This has the advantage that the friction element can be completely described by a differential equation without events. The drawback is that the system becomes stiff (about 10-20 times slower simulation) and that more material constants have to be supplied which requires more sophisticated identification. For more details, see the following references, especially (Armstrong and Canudas de Wit 1996):

Armstrong B. (1991):

Control of Machines with Friction. Kluwer Academic Press, Boston MA.

Armstrong B., and Canudas de Wit C. (1996):

Friction Modeling and Compensation. The Control Handbook, edited by W.S.Levine, CRC Press, pp. 1369-1382.

Canudas de Wit C., Olsson H., Åström K.J., and Lischinsky P. (1995):

A new model for control of systems with friction. IEEE Transactions on Automatic Control, Vol. 40, No. 3, pp. 419-425.

Optional heatPort

The dissipated energy is transported in form of heat to the optional heatPort connector that can be enabled via parameter "useHeatPort". Independently whether the heatPort is or is not enabled, the dissipated power is defined with variable "lossPower". If contact occurs at the hard stops, the lossPower is not correctly modelled at this time instant, because the hard stop would introduce a Dirac impulse in the lossPower due to the discontinuously changing kinetic energy of the mass (lossPower is the derivative of the kinetic energy at the time instant of the impact).

Extends from PartialFrictionWithStop (Base model of Coulomb friction elements with stop), Modelica.Thermal.HeatTransfer.Interfaces.PartialElementaryConditionalHeatPortWithoutT (Partial model to include a conditional HeatPort in order to dissipate losses, used for textual modeling, i.e., for elementary models).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.RelativeStates

Definition of relative state variables

Information

Usually, the absolute position and the absolute velocity of Modelica.Mechanics.Translational.Inertia models are used as state variables. In some circumstances, relative quantities are better suited, e.g., because it may be easier to supply initial values. In such cases, model RelativeStates allows the definition of state variables in the following way:

• Connect an instance of this model between two flange connectors.
• The relative position and the relative velocity between the two connectors are used as state variables.

An example is given in the next figure

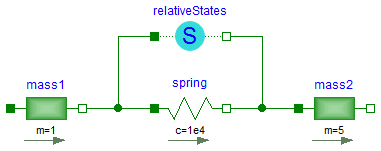
Here, the relative position and the relative velocity between the two masses are used as state variables. Additionally, the simulator selects either the absolute position and absolute velocity of model mass1 or of model mass2 as state variables.

Extends from Translational.Interfaces.PartialTwoFlanges (Component with two translational 1D flanges).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.GeneralForceToPositionAdaptor

Signal adaptor for a Translational flange with position, speed, and acceleration as outputs and force as input (especially useful for FMUs)

Information

Adaptor between a flange connector and a signal representation of the flange. This component is used to provide a pure signal interface around a Translational model and export this model in form of an input/output block, especially as FMU (Functional Mock-up Unit). Examples of the usage of this adaptor are provided in Translational.Examples.GenerationOfFMUs. This adaptor has force as input and position, velocity and acceleration as output signals.

Extends from Modelica.Blocks.Interfaces.Adaptors.FlowToPotentialAdaptor (Signal adaptor for a connector with flow, 1st derivative of flow, and 2nd derivative of flow as inputs and potential, 1st derivative of potential, and 2nd derivative of potential as outputs (especially useful for FMUs)).

Parameters

Connectors

Modelica.Mechanics.Translational.Components.GeneralPositionToForceAdaptor

Signal adaptor for a Translational flange with force as output and position, speed and acceleration as input (especially useful for FMUs)

Information

Adaptor between a flange connector and a signal representation of the flange. This component is used to provide a pure signal interface around a Translational model and export this model in form of an input/output block, especially as FMU (Functional Mock-up Unit). Examples of the usage of this adaptor are provided in Translational.Examples.GenerationOfFMUs. This adaptor has position, velocity and acceleration as input signals and force as output signal.

Note, the input signals must be consistent to each other (v=der(s), a=der(v)).

Extends from Modelica.Blocks.Interfaces.Adaptors.PotentialToFlowAdaptor (Signal adaptor for a connector with potential, 1st derivative of potential, and 2nd derivative of potential as inputs and flow, 1st derivative of flow, and 2nd derivative of flow as outputs (especially useful for FMUs)).

Parameters

Connectors