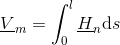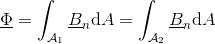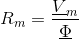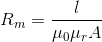This information is part of the Modelica Standard Library maintained by the Modelica Association.

Overview of the concept of quasi-static magnetic flux tubes

Following below, the concept of magnetic flux tubes is outlined in short. For a detailed description of flux tube elements, please have a look at the listed literature. Magnetic flux tubes enable the modeling of magnetic fields with lumped equivalent circuit networks.

Since quasi-static conditions are assumed, each field quantity can be represented by a complex phasor -- which is indicated by underlining the respective variable:

• Normal component of magnetic flux density,
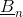
• Normal component of magnetic field strength,
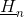
• Magnetic flux,
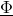
• Magnetic potential difference,

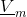
The figure below and the following equations illustrate the relationships between

• the normal component of flux density and magnetic flux, and
• the normal component of field strength and magnetic potential difference.

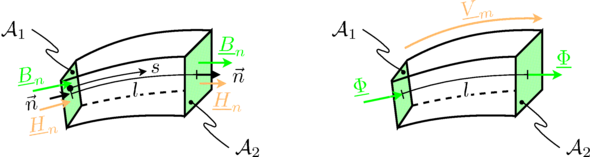
A flux tube confines the magnetic flux. Flied lines, and flux tubes, respectively are always closed. So there is no flux entering or leaving a flux tube. The total flux of a configuration can be represented by parallel flux tubes, representing different flux paths. This is considered by connecting the elements of a lumped circuit model, such that the sum of all fluxes of a connection is equivalent to zero.

For a section of a flux tube with length 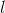the magnetic potential difference is determined by the length integral over the magnetic field strength:

The magnetic flux entering, and leaving a flux tube, respectively, is determined by the surface integral of the normal component of the magnetic field strength:

The magnetic potential difference and the magnetic flux have the same angle, so the reluctance a real (non complex) quantity:

For a generic flux tube reluctance with constant area of cross section, , and length, , the magnetic reluctance is:

Assumptions

• Force interaction is not considered
• Reluctance models are linear; so non-linearities can only be taken into account by adapting the constant relative permeability; see example NonLinearInductor

Notes

The parameter and variable names are chosen as close as possible to the transient FluxTubes library, to avoid additional effort when converting transient into quasi-static flux tubes models.

Reference Note

A similar approach on quasi-static flux tube models is published in [Raabe2012].