Modelica.Clocked.RealSignals.Sampler

Library of sampler and hold blocks for Real signals

Information

This package contains blocks that mark boundaries of a clocked partition and transform a Real signal from one partition to the next. Especially, the following blocks are provided:
 

Additionally, package Utilities contains utility blocks that are used as building blocks for user-relevant blocks. Especially, block UpSample can be used in combination with a FIR filter block to model super-sampling with interpolation and filtering.

Extends from Modelica.Icons.Package (Icon for standard packages).

Package Content

Name	Description
Sample	Sample the continuous-time, Real input signal and provide it as clocked output signal (clock is inferred)
SampleClocked	Sample the continuous-time, Real input signal and provide it as clocked output signal. The clock is provided as input signal
SampleVectorizedAndClocked	Sample the continuous-time, Real input signal vector and provide it as clocked output signal vector. The clock is provided as input signal
SampleWithADeffects	Sample with (simulated) Analog-Digital converter effects including noise
Hold	Hold the clocked, Real input signal and provide it as continuous-time output signal (zero order hold)
HoldWithDAeffects	Hold with (simulated) Digital-Analog converter effects and computational delay
SubSample	Sub-sample the clocked Real input signal and provide it as clocked output signal
SuperSample	Super-sample the clocked Real input signal and provide it as clocked output signal
SuperSampleInterpolated	Super-sample the clocked Real input signal and provide it linearly interpolated as clocked output signal (this is also called an Interpolator)
ShiftSample	Shift the clocked Real input signal by a fraction of the last interval and and provide it as clocked output signal
BackSample	Shift the clock of the Real input signal backwards in time (and access the most recent value of the input at this new clock)
AssignClock	Assign a clock to a clocked Real signal
AssignClockVectorized	Assign a clock to a clocked Real signal vector
Utilities	Utility components that are usually not directly used

Modelica.Clocked.RealSignals.Sampler.Sample

Sample the continuous-time, Real input signal and provide it as clocked output signal (clock is inferred)

Information

This block samples the continuous-time, Real input signal u and provides it as clocked output signal y. The clock of the output signal is inferred (that is, it needs to be defined somewhere else in the clocked partition). If this is not desired, use block SampleClocked instead, to explicitly assign a clock to the output signal.

To be more precise: The input signal u(t) must be a continuous-time signal. The output signal y(ti) is associated to a clock (defined somewhere else). At a clock tick, the left limit of u is assigned to y: y(ti) = u(ti-eps) (= the value of u just before the clock became active). Since the operator returns the left limit of u, it introduces an infinitesimal small delay between the continuous-time and the clocked partition. This corresponds to the reality, where a sampled data system cannot act infinitely fast and even for a very idealized simulation, an infinitesimal small delay is present. As a result, algebraic loops between clocked and continuous-time partitions cannot occur.

Examples

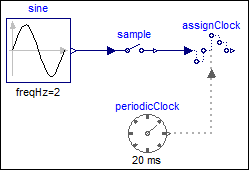
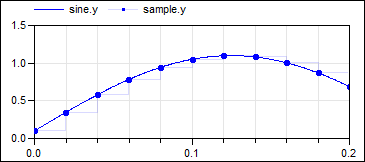
The following example samples a sine signal with a periodic clock of 20 ms period:

	model	simulation result

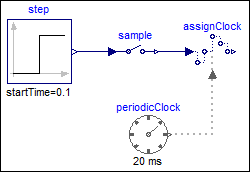
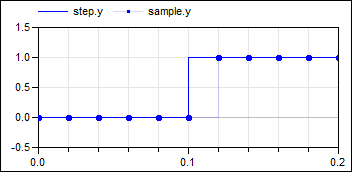
In the following example the continuous-time input signal contains a discontinuous value change at the 0.1 s clock tick. It can be seen that the Sample block samples the left limit of the step signal:

	model	simulation result

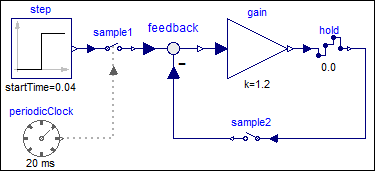
In the following example a direct feedthrough in the continuous-time and in the clocked partition is present. Without a time-delay, this would result in an algebraic loop. However, since block Sample samples the left limit of a continuous-time signal, sampling introduces a delay of one sample period that breaks the algebraic loop:

	model
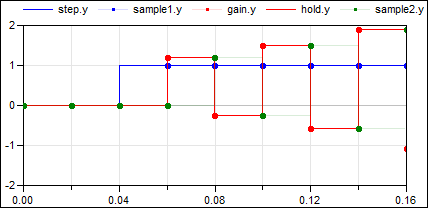
	simulation result

Note, the reason for the delay is that sample2.y (= the green, clocked signal) is the left limit of hold.y (= the red, continuous-time signal).

Extends from Clocked.RealSignals.Interfaces.PartialSISOSampler (Basic block used for sampling of Real signals).

Connectors

Modelica.Clocked.RealSignals.Sampler.SampleClocked

Sample the continuous-time, Real input signal and provide it as clocked output signal. The clock is provided as input signal

Information

This block is similar to the Sample block. The only difference is that a clock signal is provided via a second input and the output is associated to this clock.

Note, it does not make much sense to vectorize this block, because then also the clock input is vectorized. Instead, if the input signal is a vector, use block SampleVectorizedAndClocked that has a vector Real input and output, as well as a scalar clock input.

Example

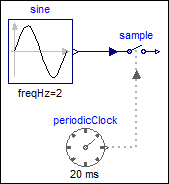
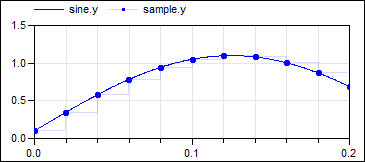
The following example samples a sine signal with a periodic clock of 20 ms period:

	model	simulation result

Extends from Clocked.RealSignals.Interfaces.SamplerIcon (Basic graphical layout of block used for sampling of Real signals).

Connectors

Modelica.Clocked.RealSignals.Sampler.SampleVectorizedAndClocked

Sample the continuous-time, Real input signal vector and provide it as clocked output signal vector. The clock is provided as input signal

Information

This block is similar to the SampleClocked block. The only difference is that the continuous-time input signal is a vector: All input signals are sampled and are associated with the scalar clock signal provided via the second input.

Example

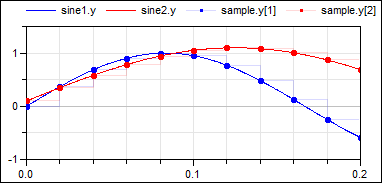
The following example has a vector as input, consisting of two different sine signals. These signals are sampled with a periodic clock of 20 ms period:

	model	simulation result

Extends from Clocked.RealSignals.Interfaces.SamplerIcon (Basic graphical layout of block used for sampling of Real signals).

Parameters

Connectors

Modelica.Clocked.RealSignals.Sampler.SampleWithADeffects

Sample with (simulated) Analog-Digital converter effects including noise

Information

This block is similar to the Sample block. The only difference is that after the sampling of the input signal, simulated real-world effects are applied on the sampled signal. In particular:

• The output is limited, if parameter limited = true.
• The output is value discretized in the form of an Analog-Digital converter with a definable number of bits, if parameters limited = true, and quantized = true.
• Noise is added to the output if parameter noisy = true. A pseudo random number generator is used to generate uniformly distributed random numbers in a given band.

Example

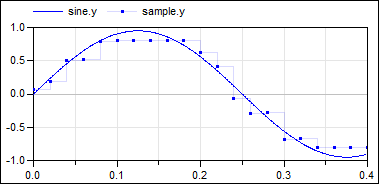
The following example samples a sine signal with a periodic clock of 20 ms period, and adds the following effects:

• Limits the output to +/- 0.8.
• Discretizes the output with an 8 bit AD converter.
• Adds large uniform noise with a band of +/- 0.2.

	model	simulation result

The output y is quite far away from the continuous-time input signal, due to the strong discretization and large noise applied to the sampled input.

Extends from Clocked.RealSignals.Interfaces.PartialSISOSampler (Basic block used for sampling of Real signals).

Parameters

Connectors

Modelica.Clocked.RealSignals.Sampler.Hold

Hold the clocked, Real input signal and provide it as continuous-time output signal (zero order hold)

Information

This block holds the clocked Real input signal u with a zero order hold and provides it as continuous-time output signal y. The clock of the input signal is inferred (that is, it needs to be defined somewhere else in the clocked partition).

To be more precise: The input signal u(ti) must be a clocked signal. The output signal y(t) is a piecewise constant continuous-time signal. When the clock of u ticks at time ti, the block output y(ti) = u(ti). Otherwise y(t), t ≥ti, is the value of u(ti) from the last clock activation at time ti. Before the first clock activation of u, the block outputs the value of parameter y_start. The value of this parameter is displayed below the icon.

Example

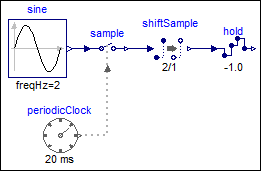
The following example samples a sine signal with a periodic clock of 20 ms period and delays it for 2 sample periods. The resulting signal is hold with the Hold block. As a result, the clock of hold.u starts ticking at 40 ms. The output hold.y of the block is a continuous-time signal that is present from the start of the simulation. Before the first tick of the clock of hold.u, it is set to -1.0 (= the value of parameter hold.y_start).

	model	simulation result

Extends from Clocked.RealSignals.Interfaces.PartialSISOHold (Basic block used for zero order hold of Real signals).

Parameters

Connectors

Modelica.Clocked.RealSignals.Sampler.HoldWithDAeffects

Hold with (simulated) Digital-Analog converter effects and computational delay

Information

This block is similar to the Hold block. The only difference is that simulated real-world effects are applied on the clocked input signal u before transforming the signal to a continuous-time signal with a zero-order hold. In particular:

• The output is delayed by a fraction of the clock period, if parameter computationalDelay = true. The delay is defined by shiftCounter/resolution*interval(), where shiftCounter and resolution are Integer parameters and interval() is the time duration from the previous to the current clock tick. The maximal possible computational delay is one clock duration, and therefore there is the restriction that shiftCounter ≤ resolution.
• The output is limited, if parameter limited = true.
• The output is value discretized in the form of an Digital-Analog converter with a definable number of bits, if parameters limited = true, and quantized = true.

Example

The following example samples a sine signal with an amplitude of 2.0 with a periodic clock of 20 ms period and delays it for 2 sample periods. The resulting signal is hold with the HoldWithDAeffects block. As a result, the clock of hold.u starts ticking at 40 ms. The output hold.y of the block is a continuous-time signal that is present from the start of the simulation. Before the first tick of the clock of hold.u, it is set to 0.5 (= the value of parameter hold.y_start). Additionally, the following effects are added to the hold block:

• The output is limited to +/- 1.9.
• A computational delay of half of a sample period (= 1/2*20 ms = 10 ms) is defined.
  

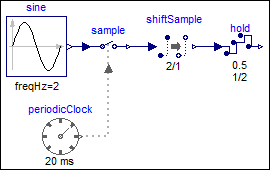	model	simulation result

Due to the limitation of the output signal, the values of hold.u ≥ 1.9 are limited to 1.9.

If the hold output is delayed by one sample period, then the previous(…) value of the input is output, and the first tick is delayed by one sample period, as shown by the modified example from above:

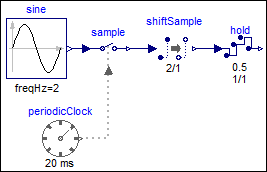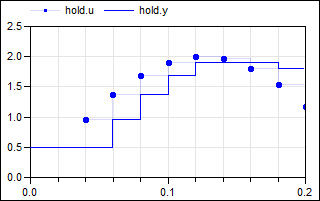	model	simulation result

Note, the computational delay of one sample period is defined by shiftCounter=1, resolution=1, as shown in the icon of the hold block.

Extends from Clocked.RealSignals.Interfaces.PartialSISOHold (Basic block used for zero order hold of Real signals).

Parameters

Connectors

Modelica.Clocked.RealSignals.Sampler.SubSample

Sub-sample the clocked Real input signal and provide it as clocked output signal

Information

This block sub-samples the clocked Real input signal u and provides it as clocked output signal y.

To be more precise: The clock of y is factor-times slower than the clock of u. At every factor ticks of the clock of u, the output y returns the value of u. The first activation of the clock of y coincides with the first activation of the clock of u. By default, the sub-sampling factor is inferred, that is, it must be defined somewhere else. If parameter inferFactor = false, then the sub-sampling factor is defined by Integer parameter factor.

Example

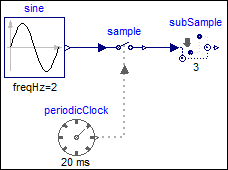
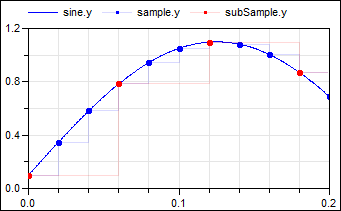
The following example samples a sine signal with a periodic clock of 20 ms period, and then sub-samples the resulting clocked signal with a factor of 3:

	model	simulation result

As can be seen, subSample.y picks every third-value of sample.y due to the sub-sampling, and the sub-sampling factor = 3 is displayed in the icon of the subSample block. Note the down-arrow in the icon of the subSample block indicates that the clock of subSample.y is slower as the clock of subSample.u.

Parameters

Connectors

Modelica.Clocked.RealSignals.Sampler.SuperSample

Super-sample the clocked Real input signal and provide it as clocked output signal

Information

This block super-samples the clocked Real input signal u and provides it as clocked output signal y.

To be more precise: The clock of y is factor-times faster than the clock of u. At every tick of the clock of y, the value of y is set to the value of u from the last tick of the clock of u. The first activation of the clock of y coincides with the first activation of the clock of u. By default, the super-sampling factor is inferred, that is, it must be defined somewhere else. If parameter inferFactor = false, then the super-sampling factor is defined by Integer parameter factor.

For control applications this block introduces unnecessary "vibrations". In such a case it is better to use block SuperSampleInterpolated instead.

Example

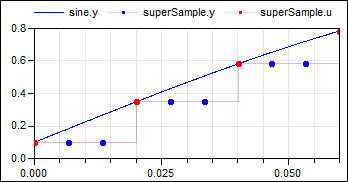
The following example samples a sine signal with a periodic clock of 20 ms period, and then super-samples the resulting clocked signal with a factor of 3:

	model	simulation result

As can be seen, superSample introduces factor-1 additional clock ticks for the output y. The super-sampling factor = 3 is displayed in the icon of the superSample block. Note the up-arrow in the icon of the superSample block indicates that the clock of superSample.y is faster as the clock of superSample.u.

Parameters

Connectors

Modelica.Clocked.RealSignals.Sampler.SuperSampleInterpolated

Super-sample the clocked Real input signal and provide it linearly interpolated as clocked output signal (this is also called an Interpolator)

Information

This block super-samples the clocked Real input signal u and provides it linearly interpolated between the u-values as clocked output signal y.

To be more precise: The clock of y is factor-times faster than the clock of u. At every tick of the clock of y, the value of y is set to the value of the linearly interpolated value between the last available values of u. The first activation of the clock of y coincides with the first activation of the clock of u. By default, the super-sampling factor is inferred, that is, it must be defined somewhere else. If parameter inferFactor = false, then the super-sampling factor is defined by Integer parameter factor.

For control applications, this block is better suited as block SuperSample since it does not induce "vibrations".

Example

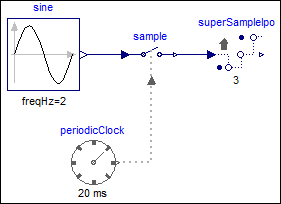
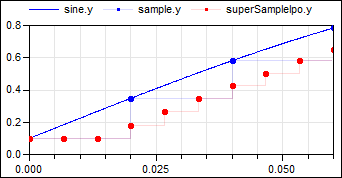
The following example samples a sine signal with a periodic clock of 20 ms period, and then super-samples the resulting clocked signal with a factor of 3 and interpolates the result linearly:

	model	simulation result

As can be seen, block superSampleIpo introduces 3 additional clock ticks for the output y and determines the values at these clock ticks, so that the last two available values of the input u are linearly interpolated. The super-sampling factor = 3 is displayed in the icon of the superSampleIpo block. Note the up-arrow in the icon of the SuperSampleInterpolation block indicates that the clock of superSampleIpo.y is faster as the clock of superSampleIpo.u.

Parameters

Connectors

Modelica.Clocked.RealSignals.Sampler.ShiftSample

Shift the clocked Real input signal by a fraction of the last interval and and provide it as clocked output signal

Information

This block shifts the first activation of the clock of the output y by fraction shiftCounter/resolution of the period (or for a non-periodic signal by a fraction of the last interval) and the output y is set to the last available value of the input u. Here, shiftCounter and resolution are positive Integer parameters.

To be more precise: The block constructs (conceptually) a clock “cBase”

Clock cBase = subSample(superSample(u, resolution), shiftCounter)

and the clock of y starts at the second clock tick of cBase. At every tick of the clock of y, the operator returns the value of u from the last tick of the clock of u.

Note, for EventClocks there is the restriction that block ShiftSample can only shift the number of ticks of the EventClock clock, but cannot introduce new ticks, due to the restriction of operator superSample on EventClocks.

Also note, that this block does not simply shift the signal in time, since only the value of u from the last tick of the clock of u is used for the output. If a time-delayed clock is desired, use instead block NonPeriodic.FractionalDelay where the input signal is delayed by a time period and old values of u are stored in a buffer. If the time delay is less than one period, the two blocks, ShiftSample and FractionalDelay, give the same result.

Example

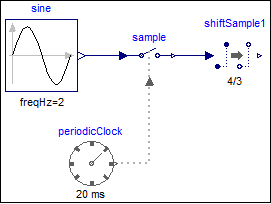
The following example samples a sine signal with a periodic clock of 20 ms period, and then shifts it with shiftCounter = 4 and resolution = 3:

	model	simulation result

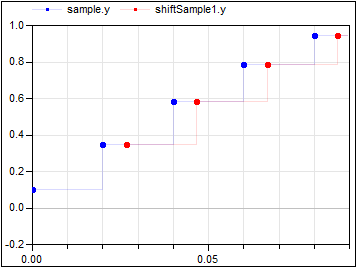
The first activation of output y of block shiftSample1 is shifted in time (4/3*20ms). The parameter values shiftCounter = 4 and resolution = 3 are visible at the bottom of the icon. Also note, that the signal is not simply a shift in time. The output of a ShiftSample block will always be the value from the last tick of the clock of its inputs.

Parameters

Connectors

Modelica.Clocked.RealSignals.Sampler.BackSample

Shift the clock of the Real input signal backwards in time (and access the most recent value of the input at this new clock)

Information

This block shifts the first activation of the clock of the output y by fraction backCounter/resolution of the period (or for a non-periodic signal by a fraction of the last interval) before the first activation of the clock of u. The output y is set to the last available value of the input u. Here, backCounter and resolution are positive Integer parameters.

To be more precise: The block constructs (conceptually) a clock “cBase”

Clock cBase = subSample(superSample(u, resolution), backCounter)

and the first clock tick of y is shifted before the first tick of the clock of u, such that this duration is identical to the duration between the first and second clock tick of cBase. Before the first tick of the clock of u, the block outputs the value of parameter y_start. After that, the block returns the last available value of u.

Note, for EventClocks there is the restriction that block BackSample can only shift the number of ticks of the EventClock clock, but cannot introduce new ticks, due to the restriction of operator superSample on EventClocks.

Also note, that this block does not simply shift the signal in time, since only the value of u from the last tick of the clock of u is used for the output. In particular, a BackSample block following a ShiftSample block cannot be used to recover the input signal of ShiftSample (for a causal system this is impossible).

Example

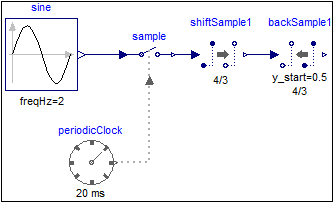
The following example samples a sine signal with a periodic clock of 20 ms period, shift-samples it with shiftCounter = 4 and resolution = 3 and then back-samples it with backCounter=4 and resolution = 3:

	model	simulation result

The first activation of output y of block backSample1 is shifted (4/3*20ms) before the first activation of output y of block shiftSample1. As a consequence, the activation times of the output y are coincident with the input signal of the shiftSample1 block. However, as described above, the output of block backSample1 does not recover the original sampled sine signal! For the first two ticks the output holds the value of the parameter y_start = 0.5. After that the output at a clock tick of block backSample1 is the last value of the output of the shiftSample1 block. The parameter values y_start = 0.5, shiftCounter = 4 and resolution = 3 are visible at the bottom of the icon.

Parameters

Connectors

Modelica.Clocked.RealSignals.Sampler.AssignClock

Assign a clock to a clocked Real signal

Information

This block assigns a clock to the Real input signal u and provides u as output signal y.

Example

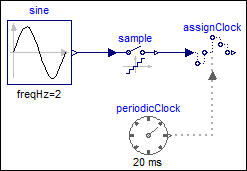
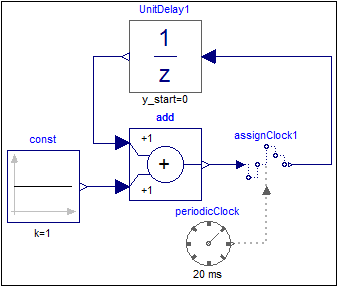
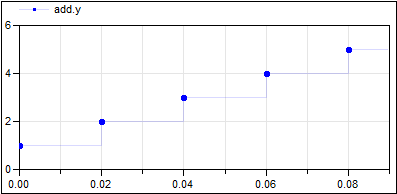
The following example shows a discrete counter. In order to execute the counter with a sample period of 20ms an AssignClock block is used. Due to clock inference all equations within the blocks are deduced to be active at the clock ticks given by the periodicClock block.

	model	simulation result

At every clock tick (that is at every 20ms) the output of the unitDelay1 block is incremented by one.

Connectors

Modelica.Clocked.RealSignals.Sampler.AssignClockVectorized

Assign a clock to a clocked Real signal vector

Information

This block assigns a clock to the Real vector input signal u and provides u as vector output signal y.

Example

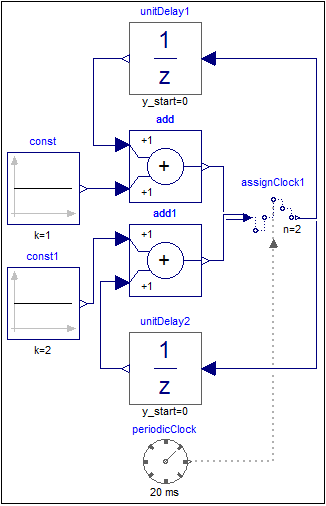
The following example shows two discrete counters. In order to execute the counters with a sample period of 20ms an AssignClockVectorized block is used. Due to clock inference all equations within the blocks are deduced to be active at the clock ticks given by the periodicClock block.

	model	simulation result

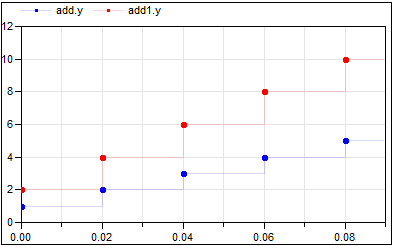
At every clock tick (that is every 20ms) the output of the unitDelay1 block is incremented by one and that of the unitDelay2 block is incremented by two. The vector size of the input and output is provided by parameter n=2 which is also shown in the icon of block assignClock1.

Parameters

Connectors