Modelica.Electrical.QuasiStatic.Polyphase.Basic

Basic components for AC polyphase models

Information

This package hosts basic models for quasi-static polyphase circuits. Quasi-static theory can be found in the references.

See also

Extends from Modelica.Icons.Package (Icon for standard packages).

Package Content

Name	Description
Star	Star connection
Delta	Delta (polygon) connection
MultiStar	Star connection of polyphase systems consisting of multiple base systems
MultiDelta	Delta (polygon) connection of polyphase systems consisting of multiple base systems
MultiStarResistance	Resistance connection of star points
PlugToPin_p	Connect one (positive) pin
PlugToPin_n	Connect one (negative) pin
PlugToPins_p	Connect all (positive) pins
PlugToPins_n	Connect all (negative) pins
Resistor	Polyphase linear resistor
Conductor	Polyphase linear conductor
Capacitor	Polyphase linear capacitor
Inductor	Polyphase linear inductor
MutualInductor	Linear mutual inductor
Impedance	Polyphase linear impedance
Admittance	Polyphase linear admittance
VariableResistor	Polyphase variable resistor
VariableConductor	Polyphase variable conductor
VariableCapacitor	Polyphase variable capacitor
VariableInductor	Polyphase variable inductor
VariableImpedance	Polyphase variable impedance
VariableAdmittance	Polyphase variable admittance

Modelica.Electrical.QuasiStatic.Polyphase.Basic.Star

Star connection

Information

Star (wye) connection of a polyphase circuit. The potentials at the star points are the same.

See also

Delta, MultiStar, MultiDelta

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.Delta

Delta (polygon) connection

Information

Delta (polygon) connection of a polyphase circuit.

See also

Star, MultiStar, MultiDelta

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.MultiStar

Star connection of polyphase systems consisting of multiple base systems

Information

Star (wye) connection of a polyphase circuit consisting of multiple base systems (see polyphase guidelines). The potentials at the star points are all equal.

See also

Star, Delta, MultiDelta

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.MultiDelta

Delta (polygon) connection of polyphase systems consisting of multiple base systems

Information

Delta (polygon) connection of a polyphase circuit consisting of multiple base systems (see polyphase guidelines).

See also

Star, Delta, MultiStar

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.MultiStarResistance

Resistance connection of star points

Information

Multi star points are connected by resistors. This model is required to operate polyphase systems with even phase numbers to avoid ideal connections of start points of base systems; see polyphase guidelines.

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.PlugToPin_p

Connect one (positive) pin

Information

Connects the single-phase (positive) pin k of the polyphase (positive) plug to a single-phase (positive) pin.

See also

PlugToPin_n, PlutToPins_p, PlugToPins_n

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.PlugToPin_n

Connect one (negative) pin

Information

Connects the single-phase (negative) pin k of the polyphase (negative) plug to a single-phase (negative) pin.

See also

PlugToPin_p, PlutToPins_p, PlugToPins_n

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.PlugToPins_p

Connect all (positive) pins

Information

Connects all m single-phase (positive) pins of the polyphase (positive) plug to an array of m single-phase (positive) pins.

See also

PlugToPin_p, PlugToPin_n, PlugToPins_n

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.PlugToPins_n

Connect all (negative) pins

Information

Connects all m single-phase (negative) pins of the polyphase (negative) plug to an array of m single-phase (negative) pins.

See also

PlugToPin_p, PlugToPin_n, PlugToPins_p

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.Resistor

Polyphase linear resistor

Information

The linear resistor connects the complex voltages v with the complex currents i by i*R = v, using m single-phase Resistors.

The resistor model also has m optional conditional heat ports. A linear temperature dependency of the resistances for enabled heat ports is also taken into account.

See also

Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance

Extends from Interfaces.TwoPlug (Two plugs with pin-adapter, reference connection and declaration of voltage and current), Modelica.Electrical.Polyphase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.Conductor

Polyphase linear conductor

Information

The linear resistor connects the complex currents i with the complex voltages v by v*G = i, using m single-phase Conductors.

The conductor model also has m optional conditional heat ports. A linear temperature dependency of the conductances for enabled heat ports is also taken into account.

See also

Conductor, Resistor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance

Extends from Interfaces.TwoPlug (Two plugs with pin-adapter, reference connection and declaration of voltage and current), Modelica.Electrical.Polyphase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.Capacitor

Polyphase linear capacitor

Information

The linear capacitor connects the complex currents i with the complex voltages v by v*j*ω*C = i, using m single-phase Capacitors.

See also

Capacitor, Resistor, Conductor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance

Extends from Interfaces.TwoPlug (Two plugs with pin-adapter, reference connection and declaration of voltage and current).

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.Inductor

Polyphase linear inductor

Information

The linear inductor connects the complex voltages v with the complex currents i by i*j*ω*L = v, using m single-phase Inductors.

See also

Inductor, Resistor, Conductor, Capacitor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance

Extends from Interfaces.TwoPlug (Two plugs with pin-adapter, reference connection and declaration of voltage and current).

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.MutualInductor

Linear mutual inductor

Information

Model of a polyphase inductor providing a mutual inductance matrix model.

Implementation

v[1] = j*omega*L[1,1]*i[1] + j*omega*L[1,2]*i[2] + ... + j*omega*L[1,m]*i[m]
v[2] = j*omega*L[2,1]*i[1] + j*omega*L[2,2]*i[2] + ... + j*omega*L[2,m]*i[m]
   :              :                     :                           :
v[m] = j*omega*L[m,1]*i[1] + j*omega*L[m,2]*i[2] + ... + j*omega*L[m,m]*i[m]

Extends from QuasiStatic.Polyphase.Interfaces.OnePort (Two plugs, reference connection and declaration of voltage and current).

Parameters

Connectors

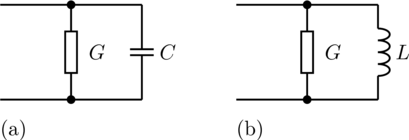
Modelica.Electrical.QuasiStatic.Polyphase.Basic.Impedance

Polyphase linear impedance

Information

The impedance model represents a series connection of a resistor and either an inductor or capacitor in each phase.

The linear impedance connects the voltage v with the current i by v = Z*i in each phase, using m single-phase impedances. The resistive components are modeled temperature dependent, so the real parts R_actual = real(Z) are determined from the actual operating temperatures and the reference input resistances real(Z_ref). Conditional heat ports are considered. The reactive components X_actual = imag(Z) are equal to imag(Z_ref) if frequencyDependent = false. Frequency dependency is considered by frequencyDependent = true, distinguishing two cases:

(a) imag(Z_ref) > 0: inductive case

The actual reactances X_actual are proportional to f/f_ref

(b) imag(Z_ref) < 0: capacitive case

The actual reactances X_actual are proportional to f_ref/f

See also

Impedance, Resistor, Conductor, Capacitor, Inductor, Admittance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance

Extends from Interfaces.TwoPlug (Two plugs with pin-adapter, reference connection and declaration of voltage and current), Modelica.Electrical.Polyphase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.Admittance

Polyphase linear admittance

Information

The admittance model represents a parallel connection of a resistor and either a capacitor or inductor in each phase.

The linear admittance connects the voltage v with the current i by i = Y*v in each phase, using m single-phase admittances. The resistive components are modeled temperature dependent, so the real parts G_actual = real(Y) are determined from the actual operating temperatures and the reference input conductances real(Y_ref). Conditional heat ports are considered. The reactive components B_actual = imag(Y) are equal to imag(Y_ref) if frequencyDependent = false. Frequency dependency is considered by frequencyDependent = true, distinguishing two cases:

(a) imag(Y_ref) > 0: capacitive case

The actual susceptances B_actual are proportional to f/f_ref

(b) imag(Y_ref) < 0: inductive case

The actual susceptances B_actual are proportional to f_ref/f

See also

Admittance, Resistor, Conductor, Capacitor, Impedance, Variable resistor, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance

Extends from Interfaces.TwoPlug (Two plugs with pin-adapter, reference connection and declaration of voltage and current), Modelica.Electrical.Polyphase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.VariableResistor

Polyphase variable resistor

Information

The linear resistors connect the complex voltages v with the complex currents i by i*R = v, using m single-phase variable Resistors. The resistances R are given as m input signals.

The resistor model also has m optional conditional heat ports. A linear temperature dependency of the resistances is also taken into account.

See also

VariableResistor, Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable conductor, Variable capacitor, Variable inductor, Variable impedance, Variable admittance

Extends from Interfaces.TwoPlug (Two plugs with pin-adapter, reference connection and declaration of voltage and current), Modelica.Electrical.Polyphase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.VariableConductor

Polyphase variable conductor

Information

The linear resistors connect the complex currents i with the complex voltages v by v*G = i, using m single-phase variable Conductors. The conductances G are given as m input signals.

The conductor model also has m optional conditional heat ports. A linear temperature dependency of the conductances is also taken into account.

See also

VariableConductor, Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable capacitor, Variable inductor Variable impedance, Variable admittance

Extends from Interfaces.TwoPlug (Two plugs with pin-adapter, reference connection and declaration of voltage and current), Modelica.Electrical.Polyphase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.VariableCapacitor

Polyphase variable capacitor

Information

The linear capacitors connect the complex currents i with the complex voltages v by v*j*ω*C = i, using m single-phase variable Capacitors. The capacitances C are given as m input signals.

See also

VariableCapacitor, Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable inductor Variable impedance, Variable admittance

Extends from Interfaces.TwoPlug (Two plugs with pin-adapter, reference connection and declaration of voltage and current).

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.VariableInductor

Polyphase variable inductor

Information

The linear inductors connect the complex voltages v with the complex currents i by i*j*ω*L = v, using m single-phase variable Inductors. The inductances L are given as m input signals.

See also

Inductor, Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable resistor, Variable conductor, Variable capacitor Variable impedance, Variable admittance

Extends from Interfaces.TwoPlug (Two plugs with pin-adapter, reference connection and declaration of voltage and current).

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.VariableImpedance

Polyphase variable impedance

Information

The impedance model represents a series connection of a resistor and either an inductor or capacitor in each phase.

The linear impedance connects the complex voltage v with the complex current i by i*Z = v in each phase, using m variable single-phase impedances. The impedances Z_ref = R_ref + j*X_ref are given as complex input signals, representing the resistive and reactive components of the input impedances. The resistive components are modeled temperature dependent, so the real part R_actual = real(Z) are determined from the actual operating temperatures and the reference input resistances real(Z_ref). Conditional heat ports are considered. The reactive components X_actual = imag(Z) are equal to imag(Z_ref) if frequencyDependent = false. Frequency dependency is considered by frequencyDependent = true, distinguishing two cases:

(a) imag(Z_ref) > 0: inductive case

The actual reactances X_actual are proportional to f/f_ref

(b) imag(Z_ref) < 0: capacitive case

The actual reactances X_actual are proportional to f_ref/f

Note

Zero crossings of the real or imaginary parts of the impedance signals Z_ref could cause singularities due to the actual structure of the connected network.

See also

VariableResistor, Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable conductor, Variable capacitor, Variable inductor Variable admittance

Extends from Interfaces.TwoPlug (Two plugs with pin-adapter, reference connection and declaration of voltage and current), Modelica.Electrical.Polyphase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).

Parameters

Connectors

Modelica.Electrical.QuasiStatic.Polyphase.Basic.VariableAdmittance

Polyphase variable admittance

Information

The admittance model represents a parallel connection of a resistor and either a capacitor or inductor in each phase.

The linear admittance connects the complex voltage v with the complex current i by v*Y = i in each phase, using m variable single-phase admittances. The admittances Y_ref = G_ref + j*B_ref are given as complex input signals, representing the resistive and reactive components of the input admittances. The resistive components are modeled temperature dependent, so the real part G_actual = real(Y) are determined from the actual operating temperatures and the reference input conductances real(Y_ref). Conditional heat ports are considered. The reactive components B_actual = imag(Y) are equal to imag(Y_ref) if frequencyDependent = false. Frequency dependency is considered by frequencyDependent = true, distinguishing two cases:

(a) imag(Y_ref) > 0: capacitive case

The actual susceptances B_actual are proportional to f/f_ref

(b) imag(Y_ref) < 0: inductive case

The actual susceptances B_actual are proportional to f_ref/f

Note

Zero crossings of the real or imaginary parts of the admittance signals Y_ref could cause singularities due to the actual structure of the connected network.

See also

VariableResistor, Resistor, Conductor, Capacitor, Inductor, Impedance, Admittance, Variable conductor, Variable capacitor, Variable inductor Variable impedance,

Extends from Interfaces.TwoPlug (Two plugs with pin-adapter, reference connection and declaration of voltage and current), Modelica.Electrical.Polyphase.Interfaces.ConditionalHeatPort (Partial model to include conditional HeatPorts in order to describe the power loss via a thermal network).

Parameters

Connectors