Basic elements of magnetic network models
Extends from Modelica.Icons.Package (Icon for standard packages).
| Name | Description |
|---|---|
| Zero magnetic potential | |
| Ideal electromagnetic energy conversion | |
| Electromagnetic energy conversion with a leakage inductance | |
| Constant reluctance | |
| Constant permeance | |
| Variable reluctance | |
| Variable permeance | |
| Leakage reluctance with respect to the reluctance of a useful flux path (not for dynamic simulation of actuators) | |
| For modelling of eddy current in a conductive magnetic flux tube | |
| Idle running branch | |
| Short cut branch | |
| Crossing of two branches |
 Modelica.Magnetic.FluxTubes.Basic.Ground
Modelica.Magnetic.FluxTubes.Basic.GroundZero magnetic potential
The magnetic potential at the magnetic ground node is zero. Every magnetic network model must contain at least one magnetic ground object.
| Name | Description |
|---|---|
| port |
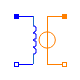 Modelica.Magnetic.FluxTubes.Basic.ElectroMagneticConverter
Modelica.Magnetic.FluxTubes.Basic.ElectroMagneticConverterIdeal electromagnetic energy conversion
The electromagnetic energy conversion is given by Ampere's law and Faraday's law respectively:
Vm = N * i N * dΦ/dt = -v
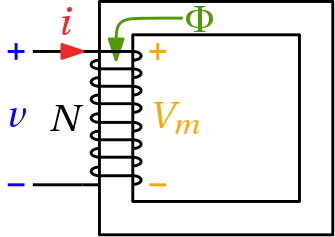
Vm is the magnetic potential difference applied to the magnetic circuit due to the current i through the coil (Ampere's law).
There exists a left-hand assignment between the current i (Put your hand around the coil, fingers pointing in the direction of current flow.)
and the magnetic potential difference Vm (thumb).
Note: There exists a right-hand assignment between the current through the coil i (fingers) and the magnetomotive force mmf.
The mmf has the opposite direction compared with Vm, it is not used in Modelica.
For the complete magnetic circuit the sum of all magnetic potential differences counted with the correct sign in a reference direction is equal to zero: sum(Vm) = 0.
The magnetic flux Φ in each passive component is related to the magnetic potential difference Vm by the equivalent of Ohms' law: Vm = Rm * Φ
Note: The magnetic resistance Rm depends on geometry and material properties. For ferromagnetic materials Rm is not constant due to saturation.
Therefore the sign (actual direction) of Φ (magnetic flux through the converter) depends on the associated branch of the magnetic circuit.
v is the induced voltage in the coil due to the derivative of magnetic flux Φ (Faraday's law).
Note: The negative sign of the induced voltage v is due to Lenz's law.
Note: The image shows a coil wound counter-clockwise (positive mathematical direction). If a coil wound clockwise has to be modeled instead, the parameter N (Number of turns) can be set to a negative value.
The flux linkage Ψ and the static inductance L_stat = |Ψ/i| are calculated for information only. Note that L_stat is set to |Ψ/eps| if |i| < eps (= 100*Modelica.Constants.eps).
| Name | Description |
|---|---|
| N | Number of turns |
| Name | Description |
|---|---|
| port_p | Positive magnetic port |
| port_n | Negative magnetic port |
| p | Positive electrical pin |
| n | Negative electrical pin |
 Modelica.Magnetic.FluxTubes.Basic.ElectroMagneticConverterWithLeakageInductance
Modelica.Magnetic.FluxTubes.Basic.ElectroMagneticConverterWithLeakageInductanceElectromagnetic energy conversion with a leakage inductance
Same as ElectroMagneticConverter with an additional leakage path on the magnetic side (leakage inductance, leakage flux). This model may improve stability especially when the magnetic circuit contains more than one electromagnetic converter.
| Name | Description |
|---|---|
| N | Number of turns |
| Leakage inductance | |
| L | Length in direction of flux [m] |
| A | Area of cross-section [m2] |
| mu_rel | Constant relative permeability of leakage inductance (> 0 required) [1] |
| Name | Description |
|---|---|
| port_p | Positive magnetic port |
| port_n | Negative magnetic port |
| p | Positive electrical pin |
| n | Negative electrical pin |
 Modelica.Magnetic.FluxTubes.Basic.ConstantReluctance
Modelica.Magnetic.FluxTubes.Basic.ConstantReluctanceConstant reluctance
This constant reluctance is provided for test purposes and simple magnetic network models. The reluctance is not calculated from geometry and permeability of a flux tube, but is provided as parameter.
Extends from Interfaces.TwoPort (Interface component including flux balance equation), Modelica.Magnetic.FluxTubes.Icons.Reluctance (Icon for reluctance / permeance components).
| Name | Description |
|---|---|
| R_m | Magnetic reluctance [H-1] |
| Initialization | |
| Phi | Magnetic flux from port_p to port_n [Wb] |
| Name | Description |
|---|---|
| port_p | Positive magnetic port |
| port_n | Negative magnetic port |
 Modelica.Magnetic.FluxTubes.Basic.ConstantPermeance
Modelica.Magnetic.FluxTubes.Basic.ConstantPermeanceConstant permeance
This constant permeance is provided for test purposes and simple magnetic network models. The permeance is not calculated from geometry and permeability of a flux tube, but is provided as parameter.
Extends from Interfaces.TwoPort (Interface component including flux balance equation), Modelica.Magnetic.FluxTubes.Icons.Reluctance (Icon for reluctance / permeance components).
| Name | Description |
|---|---|
| G_m | Magnetic permeance [H] |
| Initialization | |
| Phi | Magnetic flux from port_p to port_n [Wb] |
| Name | Description |
|---|---|
| port_p | Positive magnetic port |
| port_n | Negative magnetic port |
 Modelica.Magnetic.FluxTubes.Basic.VariableReluctance
Modelica.Magnetic.FluxTubes.Basic.VariableReluctanceVariable reluctance
The reluctance of this model is controlled by a real signal input.
Extends from Interfaces.TwoPort (Interface component including flux balance equation), Modelica.Magnetic.FluxTubes.Icons.Reluctance (Icon for reluctance / permeance components).
| Name | Description |
|---|---|
| Initialization | |
| Phi | Magnetic flux from port_p to port_n [Wb] |
| Name | Description |
|---|---|
| port_p | Positive magnetic port |
| port_n | Negative magnetic port |
| R_m | Magnetic reluctance [H-1] |
 Modelica.Magnetic.FluxTubes.Basic.VariablePermeance
Modelica.Magnetic.FluxTubes.Basic.VariablePermeanceVariable permeance
The permeance of this model is controlled by a real signal input.
Extends from Interfaces.TwoPort (Interface component including flux balance equation), Modelica.Magnetic.FluxTubes.Icons.Reluctance (Icon for reluctance / permeance components).
| Name | Description |
|---|---|
| Initialization | |
| Phi | Magnetic flux from port_p to port_n [Wb] |
| Name | Description |
|---|---|
| port_p | Positive magnetic port |
| port_n | Negative magnetic port |
| G_m | Magnetic permeance [H] |
 Modelica.Magnetic.FluxTubes.Basic.LeakageWithCoefficient
Modelica.Magnetic.FluxTubes.Basic.LeakageWithCoefficientLeakage reluctance with respect to the reluctance of a useful flux path (not for dynamic simulation of actuators)
Differently from the flux tube elements of package Shapes.Leakage that are calculated from their geometry, this leakage reluctance is calculated with reference to the total reluctance of a useful flux path. Please refer to the Parameters section for an illustration of the resulting magnetic network. Exploiting Kirchhoff's generalized current law, the leakage reluctance is calculated by means of a coupling coefficient c_usefulFlux.
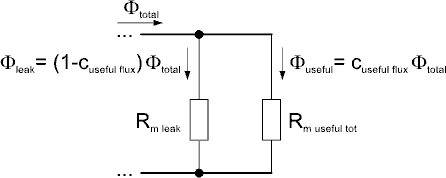
This element must not be used for dynamic simulation of electro-magneto-mechanical actuators, where the shape of at least one flux tube element with reluctance force generation in the useful flux path changes with armature motion (e.g., air gap). This change results in a non-zero derivative dG_m/dx of those elements permeance G_m with respect to armature position x, which in turn will lead to a non-zero derivative of the leakage permeance with respect to armature position. This would generate a reluctance force in the leakage element that is not accounted for properly. Shapes.Force.LeakageAroundPoles provides a simple leakage reluctance with force generation.
Extends from BaseClasses.Leakage (Base class for leakage flux tubes with position-independent permeance and hence no force generation; mu_r=1).
| Name | Description |
|---|---|
| c_usefulFlux | Ratio useful flux/(leakage flux + useful flux) = useful flux/total flux [1] |
 | |
| Initialization | |
| Phi | Magnetic flux from port_p to port_n [Wb] |
| Name | Description |
|---|---|
| port_p | Positive magnetic port |
| port_n | Negative magnetic port |
| R_mUsefulTot | [H-1] |
 Modelica.Magnetic.FluxTubes.Basic.EddyCurrent
Modelica.Magnetic.FluxTubes.Basic.EddyCurrentFor modelling of eddy current in a conductive magnetic flux tube
Eddy currents are induced in a conductive magnetic flux tube when the flux changes with time. This causes a magnetic voltage drop in addition to the voltage drop that is due to the reluctance of this flux tube. The eddy current component can be thought of as a short-circuited secondary winding of a transformer with only one turn. Its resistance is calculated from the geometry and resistivity of the eddy current path.
Partitioning of a solid conductive cylinder or prism into several hollow cylinders or separate nested prisms and modelling of each of these flux tubes connected in parallel with a series connection of a reluctance element and an eddy current component can model the delayed buildup of the magnetic field in the complete flux tube from the outer to the inner sections. Please refer to [Ka08] for an illustration.
Extends from Interfaces.TwoPort (Interface component including flux balance equation), Modelica.Electrical.Analog.Interfaces.ConditionalHeatPort (Partial model to include a conditional HeatPort in order to describe the power loss via a thermal network).
| Name | Description |
|---|---|
| useHeatPort | = true, if heatPort is enabled |
| T | Fixed device temperature if useHeatPort = false [K] |
| useConductance | Use conductance instead of geometry data and rho |
| G | Equivalent loss conductance G=A/rho/l [S] |
| rho | Resistivity of flux tube material (default: Iron at 20degC) [Ohm.m] |
| l | Average length of eddy current path [m] |
| A | Cross sectional area of eddy current path [m2] |
| Initialization | |
| Phi | Magnetic flux from port_p to port_n [Wb] |
| Name | Description |
|---|---|
| port_p | Positive magnetic port |
| port_n | Negative magnetic port |
| heatPort | Conditional heat port |
 Modelica.Magnetic.FluxTubes.Basic.Idle
Modelica.Magnetic.FluxTubes.Basic.IdleIdle running branch
This is a simple idle running branch.
Extends from Interfaces.TwoPort (Interface component including flux balance equation).
| Name | Description |
|---|---|
| Initialization | |
| Phi | Magnetic flux from port_p to port_n [Wb] |
| Name | Description |
|---|---|
| port_p | Positive magnetic port |
| port_n | Negative magnetic port |
 Modelica.Magnetic.FluxTubes.Basic.Short
Modelica.Magnetic.FluxTubes.Basic.ShortShort cut branch
This is a simple short cut branch.
Extends from Interfaces.TwoPortElementary (Interface component with two magnetic ports for textual programming).
| Name | Description |
|---|---|
| port_p | Positive magnetic port |
| port_n | Negative magnetic port |
 Modelica.Magnetic.FluxTubes.Basic.Crossing
Modelica.Magnetic.FluxTubes.Basic.CrossingCrossing of two branches
This is a simple crossing of two branches. The ports port_p1 and port_p2 are connected, as well as port_n1 and port_n2.
| Name | Description |
|---|---|
| port_p1 | Positive port_p1 connected with port_p2 |
| port_p2 | Positive port_p2 connected with port_p1 |
| port_n1 | Negative port_n1 connected with port_n2 |
| port_n2 | Negative port_n2 connected with port_n1 |