UserDefinedGravityFieldDemonstrate the modeling of a user-defined gravity field |
|
Diagram
Information
This information is part of the Modelica Standard Library maintained by the Modelica Association.
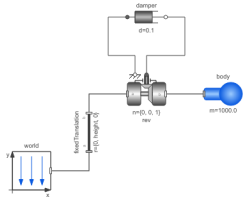
This example demonstrates a user defined gravity field. Function "world.gravityAcceleration" is redeclared to function theoreticalNormalGravityWGS84 that computes the theoretical gravity of the WGS84 ellipsoid earth model at and close to the earth ellipsoid surface. In the gravity field, a large, single pendulum is present. Via parameter "geodeticLatitude", the geodetic latitude on the earth can be defined, where the pendulum is present. The world frame is located at the WGS84 earth ellipsoid at this latitude. The result variable "gravity" is the gravity vector at the center of mass of the pendulum mass. Since the height of this mass is changing, the value of the gravity is also changing (the difference is in the order of 0.00001).
The result of the simulation is slightly different at the equator (geodeticLatitude=0) and at the poles (geodeticLatitude=90). For example, after 10 s of simulation time the rotation angle of the pendulum, rev.phi, has the following values:
| latitude [deg] | rev.phi [rad] |
| = 0 | = -2.39 rad |
| = 90 | = -2.42 rad |
Parameters (2)
Components (5)
| world |
Type: World |
|
|---|---|---|
| rev |
Type: Revolute |
|
| damper |
Type: Damper |
|
| body |
Type: Body |
|
| fixedTranslation |
Type: FixedTranslation |